练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在⊙O中，弦AB=1，点C在AB上移动，连结OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为___．

    【答案】

    【解析】

    作OH⊥AB，延长DC交⊙O于E，如图，根据垂径定理得到AH=BH=AB=，CD=CE，再判断出△BCD∽△ECA得出CDCE=BCAC，易得CD=，当CH最小时，CD最大，C点运动到H点时，CH最小，所以CD的最大值为．

    解：作OH⊥AB，延长DC交⊙O于E，如图，

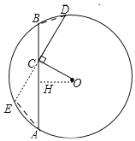
    ∴AH=BH=AB=，

    ∵CD⊥OC，

    ∴CD=CE，

    ∵∠ABD=∠DEA，∠BCD=∠ECA，

    ∴△BCD∽△ECA，

    ∴，

    ∴CDCE=BCAC，

    ∴CD2=（BH-CH）（AH+CH）=（-CH）（+CH）=-CH2，

    ∴CD=，

    ∴当CH最小时，CD最大，

    而C点运动到H点时，CH最小，

    此时CD=，即CD的最大值为．

    故答案为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】定义：若一次函数y=ax+b和反比例函数y=-满足a+c=2b，则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数．

    （1）判断y=x+b和y=-是否存在“等差”函数？若存在，写出它们的“等差”函数；

    （2）若y=5x+b和y=-存在“等差”函数，且“等差”函数的图象与y=-的图象的一个交点的横坐标为1，求一次函数和反比例函数的表达式；

    （3）若一次函数y=ax+b和反比例函数y=-（其中a＞0，c＞0，a=b）存在“等差”函数，且y=ax+b与“等差”函数有两个交点A（x1，y1）、B（x2，y2），试判断“等差”函数图象上是否存在一点P（x，y）（其中x1＜x＜x2），使得△ABP的面积最大？若存在，用c表示△ABP的面积的最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

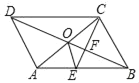
    【题目】如图，ABCD的对角线AC，BD交于点O，CE平分∠BCD交AB于点E，交BD于点F，且∠ABC＝60°，AB＝2BC，连接OE．下列结论：①∠ACD＝30°；②SABCD＝ACBC；③OE：AC＝：6； ④SOEF＝SABCD，成立的是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一袋装有编号为1，2，3的三个形状、大小、材质等相同的小球，从袋中随意摸出1个球，记事件A为“摸出的球编号为奇数”，随意抛掷一个之地均匀正方体骰子，六个面上分别写有1﹣6这6个整数，记事件B为“向上一面的数字是3的整数倍”，请你判断等式“P（A）=2P（B）”是否成立，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】费尔兹奖是国际上享有崇高荣誉的一个数学奖项，每4年评选一次，在国际数学家大会上颁给有卓越贡献的年龄不超过40岁的年轻数学家，美籍华人丘成桐1982年获得费尔兹奖．为了让学生了解费尔兹奖得主的年龄情况，我们查取了截止到2018年60名费尔兹奖得主获奖时的年龄数据，并对数据进行整理、描述和分析．下面给出了部分信息．

    a．截止到2018年费尔兹奖得主获奖时的年龄数据的频数分布直方图如图1（数据分成5组，各组是28≤x＜31，31≤x＜34，34≤x＜37，37≤x＜40，x≥40）：

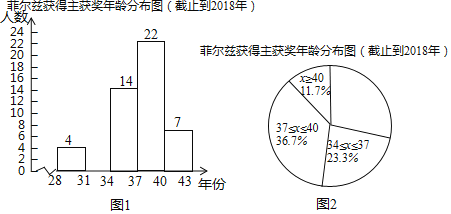
    b．如图2，在a的基础上，画出扇形统计图；

    c．截止到2018年费尔兹奖得主获奖时的年龄在34≤x＜37这一组的数据是：

    36

    35

    34

    35

    35

    34

    34

    35

    36

    36

    36

    36

    34

    35

    d．截止到2018年时费尔兹奖得主获奖时的年龄的平均数、中位数、众数如下：

    年份

    平均数

    中位数

    众数

    截止到2018

    35.58

    m

    37，38

    根据以上信息，回答下列问题：

    （1）依据题意，补全频数直方图；

    （2）31≤x＜34这组的圆心角度数是度，并补全扇形统计图；

    （3）统计表中中位数m的值是；

    （4）根据以上统计图表试描述费尔兹奖得主获奖时的年龄分布特征．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某农作物的生长率P与温度t(℃)有如下关系：如图1，当10≤t≤25时可近似用函数刻画；当25≤t≤37时可近似用函数刻画．

    (1)求h的值．

    (2)按照经验，该作物提前上市的天数m(天)与生长率P满足函数关系：

    生长率P

    0.2

    0.25

    0.3

    0.35

    提前上市的天数m（天）

    0

    5

    10

    15

    ①请运用已学的知识，求m关于P的函数表达式；

    ②请用含的代数式表示m ；

    (3)天气寒冷，大棚加温可改变农作物生长速度．在(2)的条件下，原计划大棚恒温20℃时，每天的成本为200元，该作物30天后上市时，根据市场调查：每提前一天上市售出(一次售完)，销售额可增加600元．因此给大棚继续加温，加温后每天成本w(元)与大棚温度t(℃)之间的关系如图2．问提前上市多少天时增加的利润最大？并求这个最大利润（农作物上市售出后大棚暂停使用）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

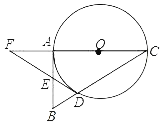
    【题目】如图，在△ABC中，∠BAC＝90°，以AC为直径的⊙O交BC于点D，点E在AB上，连接DE并延长交CA的延长线于点F，且∠AEF＝2∠C．

    （1）判断直线FD与⊙O的位置关系，并说明理由；

    （2）若AE＝2，EF＝4，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝ax2+4x+c，当x＝﹣2时，y＝﹣5；当x＝1时，y＝4

    (1)求这个二次函数表达式．

    (2)此函数图象与x轴交于点A，B(A在B的左边)，与y轴交于点C，求点A，B，C点的坐标及△ABC的面积．

    (3)该函数值y能否取到﹣6？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

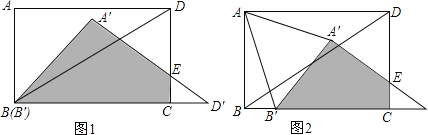
    【题目】如图，在矩形ABCD中，AB＝6cm，AD＝8cm，连接BD，将△ABD绕B点作顺时针方向旋转得到△A′B′D′（B′与B重合），且点D′刚好落在BC的延长上，A′D′与CD相交于点E．

    （1）求矩形ABCD与△A′B′D′重叠部分（如图1中阴影部分A′B′CE）的面积；

    （2）将△A′B′D′以每秒2cm的速度沿直线BC向右平移，如图2，当B′移动到C点时停止移动．设矩形ABCD与△A′B′D′重叠部分的面积为y，移动的时间为x，请你直接写出y关于x的函数关系式，并指出自变量x的取值范围；

    （3）在（2）的平移过程中，是否存在这样的时间x，使得△AA′B′成为等腰三角形？若存在，请你直接写出对应的x的值，若不存在，请你说明理由．

    查看答案和解析>>

    同步练习册答案