
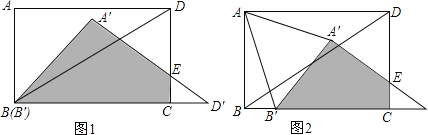
����Ŀ����ͼ���ھ���ABCD�У�AB��6cm��AD��8cm������BD������ABD��B����˳ʱ�뷽����ת�õ���A��B��D�䣨B����B�غϣ����ҵ�D��պ�����BC���ӳ��ϣ�A��D����CD�ཻ�ڵ�E��
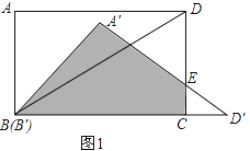
��1�������ABCD���A��B��D���ص����֣���ͼ1����Ӱ����A��B��CE���������
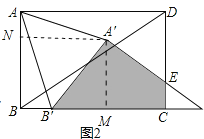
��2������A��B��D����ÿ��2cm���ٶ���ֱ��BC����ƽ�ƣ���ͼ2����B���ƶ���C��ʱֹͣ�ƶ��������ABCD���A��B��D���ص����ֵ����Ϊy���ƶ���ʱ��Ϊx������ֱ��д��y����x�ĺ�����ϵʽ����ָ���Ա���x��ȡֵ��Χ��
��3���ڣ�2����ƽ�ƹ����У��Ƿ����������ʱ��x��ʹ�á�AA��B���Ϊ���������Σ������ڣ�����ֱ��д����Ӧ��x��ֵ���������ڣ�����˵�����ɣ�
���𰸡���1��![]() ����2�������������3��ʹ�á�AA��B���Ϊ���������ε�x��ֵ�У�0�롢
����2�������������3��ʹ�á�AA��B���Ϊ���������ε�x��ֵ�У�0�롢![]() �롢
�롢![]() ��
��
��������
��1��������ת�����ʿ�֪B��D�䣽BD��10��CD�䣽B��D�䩁BC��2����tan��B��D��A�䣽![]() �����CE�����ɼ����CED��������SABCE��SABD����SCED����
�����CE�����ɼ����CED��������SABCE��SABD����SCED����
��2���������ۣ���0��x��![]() ʱ�͵�
ʱ�͵�![]() ��x��4ʱ���ֱ��г���������ʽ��
��x��4ʱ���ֱ��г���������ʽ��
��3���������ۣ���AB�䣽A��B��ʱ����AA�䣽A��B��ʱ����AB�䣽AA��ʱ�����ݹ��ɶ����з��̼��ɣ�
�⣺��1����AB��6cm��AD��8cm��
��BD��10cm��
������ת�����ʿ�֪B��D�䣽BD��10cm��CD�䣽B��D�䩁BC��2cm��
��tan��B��D��A�䣽![]()
��![]()
��CE��![]() cm��
cm��
��S ABCE��SABD����SCED����![]() ��cm2����
��cm2����
��2������0��x��![]() ʱ��CD�䣽2x+2��CE��
ʱ��CD�䣽2x+2��CE��![]() ��x+1����
��x+1����
��S��CD��E��![]() x2+3x+
x2+3x+![]() ��
��
��y��![]() ��6��8��
��6��8��![]() x2��3x��
x2��3x��![]() ����
����![]() x2��3x+
x2��3x+![]() ��
��
����![]() ��x��4ʱ��B��C��8��2x��CE��
��x��4ʱ��B��C��8��2x��CE��![]() ��8��2x��
��8��2x��
��![]() ��
��![]() x2��
x2��![]() x+
x+![]() ��
��
��3������ͼ1����AB�䣽A��B��ʱ��x��0�룻
����ͼ2����AA�䣽A��B��ʱ��A��N��BM��BB��+B��M��2x+![]() ��A��M��NB��
��A��M��NB��![]() ��
��
��AN2+A��N2��36��
�ࣨ6��![]() ��2+��2x+
��2+��2x+![]() ��2��36��
��2��36��
��ã�x��![]() ��x��
��x��![]() ����ȥ����
����ȥ����
����ͼ2����AB�䣽AA��ʱ��A��N��BM��BB��+B��M��2x+![]() ��A��M��NB��
��A��M��NB��![]() ��
��
��AB2+BB��2��AN2+A��N2
��36+4x2����6��![]() ��2+��2x+
��2+��2x+![]() ��2
��2
��ã�x��![]() ��
��
����������ʹ�á�AA��B���Ϊ���������ε�x��ֵ�У�0�롢![]() �롢
�롢![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O�У���AB=1����C��AB���ƶ�������OC������C��CD��OC����O�ڵ�D����CD�����ֵΪ___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲μ�2018���ȫ����������ѧ����������ʦ���ú��ٰѼס�������ͬѧ��ǰ���ѧ�ڵ���ѧ�ɼ�(��λ����)ͳ�Ƴ��±���
��һѧ�� | �ڶ�ѧ�� | ����ѧ�� | ����ѧ�� | ����ѧ�� | |
�� | 75 | 80 | 85 | 90 | 95 |
�� | 95 | 87 | 88 | 80 | 75 |
(1)�ֱ�����ס�������ͬѧǰ���ѧ�ڵ���ѧƽ���ɼ���
(2)��ͼ�зֱ��ס�������ͬѧǰ���ѧ�ڵ���ѧ�ɼ�������ͳ��ͼ��
(3)�����������ʦ������ΪӦ��������ѧ���μ���ѧ���������Ҫ˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
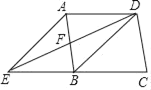
����Ŀ����ͼ����ƽ���ı���ABCD�У�DB��DA����ADB�Ľ�ƽ������AB�ཻ�ڵ�F����CB���ӳ����ཻ�ڵ�E����AE��
��1����֤���ı���AEBD�����Σ�
��2�����ı���ABCD�����Σ�DC��10��������AEBD��������� ������ֱ����գ�����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
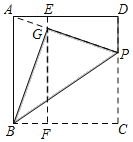
����Ŀ����ͼ����һ�ž���ֽƬABCD�У�AB��6cm����E��F�ֱ���AD��BC�����ȷֵ㣬�ֽ�����ֽƬ�۵���ʹ��C����EF�ϵĵ�G�����ۺ�ΪBP����PG���ӳ���ǡ�þ�����A����AD�ij�Ϊ_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ����A��1��4����B��4��n�����㣮
��ͼ����A��1��4����B��4��n�����㣮

��1������������һ�κ����Ľ���ʽ��
��2��ֱ��д����x��0ʱ��![]() �Ľ⼯��
�Ľ⼯��
��3����P��x���ϵ�һ���㣬��ȷ����P������������꣬ʹPA+PB��С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
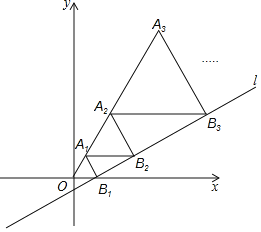
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y��![]() ��x�ύ�ڵ�B1����OB1Ϊ�߳����ȱ�������A1OB1������A1��A1B2ƽ����x�ᣬ��ֱ���ڵ�B2����A1B2Ϊ�߳����ȱ�������A2A1B2������A2��A2B3ƽ����x�ᣬ��ֱ��l�ڵ�B3����A2B3Ϊ�߳����ȱ�������A3A2B3���������A2019�ĺ������ǣ�������
��x�ύ�ڵ�B1����OB1Ϊ�߳����ȱ�������A1OB1������A1��A1B2ƽ����x�ᣬ��ֱ���ڵ�B2����A1B2Ϊ�߳����ȱ�������A2A1B2������A2��A2B3ƽ����x�ᣬ��ֱ��l�ڵ�B3����A2B3Ϊ�߳����ȱ�������A3A2B3���������A2019�ĺ������ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
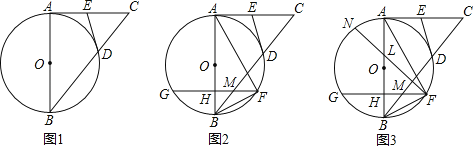
����Ŀ����֪����ͼ��ABΪ��O��ֱ����AC���O�����ڵ�A������BC��Բ�ڵ�D������D����O�����߽�AC��E��
��1����֤��AE��CE
��2����ͼ���ڻ�BD����ȡһ��F����AF����GF��AB����H����BC����M����֤����FAB+��FBM����EDC��
��3����ͼ���ڣ�2���������£���GH��FH��HM��MFʱ��tan��ABC��![]() ��DE��
��DE��![]() ʱ��NΪԲ��һ�㣬����FN��AB��L�������NFH+��CAF����AHG����LN�ij���
ʱ��NΪԲ��һ�㣬����FN��AB��L�������NFH+��CAF����AHG����LN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ҫ����ͼ����Ҫ��д��������Ҫ������ͼ�ۼ�.
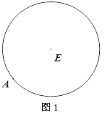
��1����ͼ1��AΪԲE��һ�㣬����ֱ�ߣ������̶ȣ���Բ������Բ�ڽ������Σ�
��2������֪���������ξ������ʣ����ߵĴ�ֱƽ�����ཻ��ͬһ�㣬������ƽ�����ཻ��һ�㣬���������ཻ��һ�㣬��ʵ�ϣ������λ��������ʣ������߽���ͬһ�㣬�������������ʣ�ֻ��ֱ�ߣ������̶ȣ���ͼ��
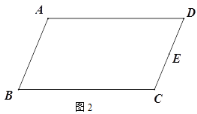
����ͼ2������ABCD�У�EΪCD���е㣬��BC���е�F;
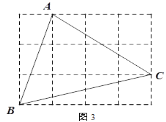
��ͼ3������С��������ɵ������У��Ķ��㶼��С�����εĶ����ϣ�����ABC�ĸ�AH
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com