
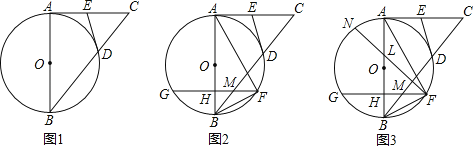
【题目】已知:如图,AB为⊙O的直径,AC与⊙O相切于点A,连接BC交圆于点D,过点D作⊙O的切线交AC于E.
(1)求证:AE=CE
(2)如图,在弧BD上任取一点F连接AF,弦GF与AB交于H,与BC交于M,求证:∠FAB+∠FBM=∠EDC.
(3)如图,在(2)的条件下,当GH=FH,HM=MF时,tan∠ABC=![]() ,DE=
,DE=![]() 时,N为圆上一点,连接FN交AB于L,满足∠NFH+∠CAF=∠AHG,求LN的长.
时,N为圆上一点,连接FN交AB于L,满足∠NFH+∠CAF=∠AHG,求LN的长.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)由直径所对的圆周角是直角,得∠ADC=90°,由切线长定理得EA=ED,再由等角的余角相等,得到∠C=∠EDC,进而得证结论.
(2)由同角的余角相等,得到∠BAD=∠C,再通过等量代换,角的加减进而得证结论.
(3)先由条件得到AB=26,设HM=FM=a,GH=HF=2a,BH=![]() a,再由相交弦定理得到GHHF=BHAH,从而求出FH,BH,AH,再由角的关系得到△HFL∽△HAF,从而求出HL,AL,BL,FL,再由相交弦定理得到LNLF=ALBL,进而求出LN的长.
a,再由相交弦定理得到GHHF=BHAH,从而求出FH,BH,AH,再由角的关系得到△HFL∽△HAF,从而求出HL,AL,BL,FL,再由相交弦定理得到LNLF=ALBL,进而求出LN的长.
解:
(1)证明:如图1中,连接AD.
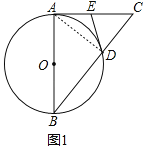
∵AB是直径,
∴∠ADB=∠ADC=90°,
∵EA、ED是⊙O的切线,
∴EA=ED,
∴∠EAD=∠EDA,
∵∠C+∠EAD=90°,∠EDC+∠EDA=90°,
∴∠C=∠EDC,
∴ED=EC,
∴AE=EC.
(2)证明:如图2中,连接AD.

∵AC是切线,AB是直径,
∴∠BAC=∠ADB=90°,
∴∠BAD+∠CAD=90°,∠CAD+∠C=90°,
∴∠BAD=∠C,
∵∠EDC=∠C,
∴∠BAD=∠EDC,
∵∠DBF=∠DAF,
∴∠FBM+∠FAB=∠FBM+∠DAF=∠BAD,
∴∠FAB+∠FBM=∠EDC.
(3)解:如图3中,

由(1)可知,DE=AE=EC,∵DE=![]() ,
,
∴AC=![]() ,
,
∵tan∠ABC=![]() =
=![]() ,
,
∴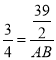 ,
,
∴AB=26,
∵GH=FH,HM=FN,设HM=FM=a,GH=HF=2a,BH=![]() a,
a,
∵GHHF=BHAH,
∴4a2=![]() a(26﹣
a(26﹣![]() a),
a),
∴a=6,
∴FH=12,BH=8,AH=18,
∵GH=HF,
∴AB⊥GF,
∴∠AHG=90°,
∵∠NFH+∠CAF=∠AHG,
∴∠NFH+∠CAF=90°,
∵∠NFH+∠HLF=90°,
∴∠HLF=∠CAF,
∵AC∥FG,
∴∠CAF=∠AFH,
∴∠HLF=∠AFH,
∵∠FHL=∠AHF,
∴△HFL∽△HAF,
∴FH2=HLHA,
∴122=HL18,
∴HL=8,
∴AL=10,BL=16,FL=![]() =4
=4![]() ,
,
∵LNLF=ALBL,
∴4![]() LN=1016,
LN=1016,
∴LN=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+4x+c,当x=﹣2时,y=﹣5;当x=1时,y=4
(1)求这个二次函数表达式.
(2)此函数图象与x轴交于点A,B(A在B的左边),与y轴交于点C,求点A,B,C点的坐标及△ABC的面积.
(3)该函数值y能否取到﹣6?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
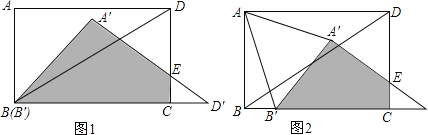
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,连接BD,将△ABD绕B点作顺时针方向旋转得到△A′B′D′(B′与B重合),且点D′刚好落在BC的延长上,A′D′与CD相交于点E.
(1)求矩形ABCD与△A′B′D′重叠部分(如图1中阴影部分A′B′CE)的面积;
(2)将△A′B′D′以每秒2cm的速度沿直线BC向右平移,如图2,当B′移动到C点时停止移动.设矩形ABCD与△A′B′D′重叠部分的面积为y,移动的时间为x,请你直接写出y关于x的函数关系式,并指出自变量x的取值范围;
(3)在(2)的平移过程中,是否存在这样的时间x,使得△AA′B′成为等腰三角形?若存在,请你直接写出对应的x的值,若不存在,请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
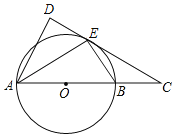
【题目】如图,AB是⊙O的直径,E是⊙O上一点,C在AB的延长线上,AD⊥CE交CE的延长线于点D,且AE平分∠DAC.
(1)求证:CD是⊙O的切线;
(2)若AB=6,∠ABE=60°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(x﹣a)(x+5)=x2﹣bx﹣5,一元二次方程ax2+bx+k=0的两个实数根x1,x2满足![]() (x1﹣x2)2﹣2x1x2=4,则k=_____.
(x1﹣x2)2﹣2x1x2=4,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
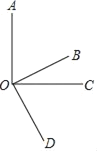
【题目】如图,射线OB、OC在∠AOD的内部,下列说法:
①若∠AOC=∠BOD=90°,则与∠BOC互余的角有2个;
②若∠AOD+∠BOC=180°,则∠AOC+∠BOD=180°;
③若OM、ON分别平分∠AOD,∠BOD,则∠MON=![]() ∠AOB;
∠AOB;
④若∠AOD=150°、∠BOC=30°,作∠AOP=![]() ∠AOB、∠DOQ=
∠AOB、∠DOQ=![]() ∠COD,则∠POQ=90°
∠COD,则∠POQ=90°
其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现需了解2019年各月份中5至14日广州市每天最低气温的情况:图①是3月份的折线统计图.(数据来源于114天气网)
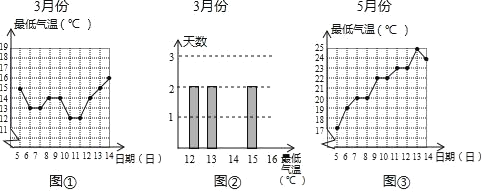
(1)图②是3月份的频数分布直方图,根据图①提供的信息,补全图②中的频数分布直方图;
(2)3月13日与10日这两天的最低气温之差是 ℃;
(3)图③是5月份的折线统计图.用![]() 表示5月份的方差;用
表示5月份的方差;用![]() 表示3月份的方差,比较大小:
表示3月份的方差,比较大小:![]()
![]() ;比较3月份与5月份, 月份的更稳定.
;比较3月份与5月份, 月份的更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分別交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为____________°

查看答案和解析>>
科目:初中数学 来源: 题型:
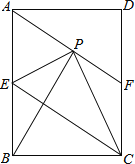
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接AP并延长AP交CD于F点,连接BP.
(1)求证:四边形AECF为平行四边形;
(2)若BC=![]() AB,判断△ABP的形状,并证明你的结论.
AB,判断△ABP的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com