
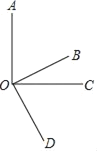
【题目】如图,射线OB、OC在∠AOD的内部,下列说法:
①若∠AOC=∠BOD=90°,则与∠BOC互余的角有2个;
②若∠AOD+∠BOC=180°,则∠AOC+∠BOD=180°;
③若OM、ON分别平分∠AOD,∠BOD,则∠MON=![]() ∠AOB;
∠AOB;
④若∠AOD=150°、∠BOC=30°,作∠AOP=![]() ∠AOB、∠DOQ=
∠AOB、∠DOQ=![]() ∠COD,则∠POQ=90°
∠COD,则∠POQ=90°
其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
根据余角和补角的定义和角平分线的定义进行计算即可得到结论.
④要分两种情况讨论. ∠AOP、∠DOQ是在内部还是外部.
解:①∵∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC=90°,
∴与∠BOC互余的角有2个;正确;
②∵∠AOD+∠BOC=∠AOB+∠BOC+∠COD+∠BCO=∠AOC+∠BOD=180°,
∴∠AOC+∠BOD=180°;故正确;
③如图1,
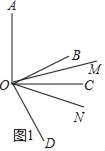
∵OM、ON分别平分∠AOD,∠BOD,
∴∠DOM=![]() ∠AOD,∠DON=
∠AOD,∠DON=![]() ∠BOD,
∠BOD,
∴∠MON=∠DOM﹣∠DON=![]() (∠AOD﹣∠BOD)=∠AOB,故正确;
(∠AOD﹣∠BOD)=∠AOB,故正确;
④如图2,
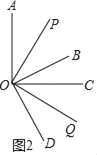
∵∠AOD=150°、∠BOC=30°,
∴∠AOB+∠COD=150°﹣30°=120°,
∵∠AOP=![]() ∠AOB、∠DOQ=
∠AOB、∠DOQ=![]() ∠COD,
∠COD,
∴∠AOP+∠DOQ=![]() (∠AOB+∠COD)=60°,
(∠AOB+∠COD)=60°,
∴∠POQ=150°﹣60°=90°,
如图3,
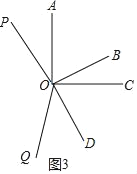
∵∠AOD=150°、∠BOC=30°,
∴∠AOB+∠COD=150°﹣30°=120°,
∵∠AOP=![]() ∠AOB、∠DOQ=
∠AOB、∠DOQ=![]() ∠COD,
∠COD,
∴∠AOP+∠DOQ=![]() (∠AOB+∠COD)=60°,
(∠AOB+∠COD)=60°,
∴∠POQ=150°+60°=210°,
综上所述,∠POQ=90°或210°,故错误.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次,掷第一次,将朝上一面的点数记为![]() ,掷第二次,将朝上一面的点数记为
,掷第二次,将朝上一面的点数记为![]() ,则点(
,则点(![]() )落在直线
)落在直线![]() 上的概率为:
上的概率为:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
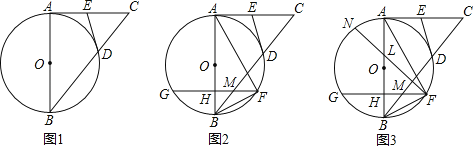
【题目】已知:如图,AB为⊙O的直径,AC与⊙O相切于点A,连接BC交圆于点D,过点D作⊙O的切线交AC于E.
(1)求证:AE=CE
(2)如图,在弧BD上任取一点F连接AF,弦GF与AB交于H,与BC交于M,求证:∠FAB+∠FBM=∠EDC.
(3)如图,在(2)的条件下,当GH=FH,HM=MF时,tan∠ABC=![]() ,DE=
,DE=![]() 时,N为圆上一点,连接FN交AB于L,满足∠NFH+∠CAF=∠AHG,求LN的长.
时,N为圆上一点,连接FN交AB于L,满足∠NFH+∠CAF=∠AHG,求LN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
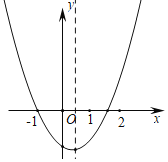
【题目】如图,函数y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0)、(m,0),且1<m<2,下列结论:①abc>0;②0<![]() <
<![]() ;③若点A(﹣3,y1),B(3,y2)在抛物线上,则y1<y2;④a(m﹣1)+b=0.其中结论正确的有( )个.
;③若点A(﹣3,y1),B(3,y2)在抛物线上,则y1<y2;④a(m﹣1)+b=0.其中结论正确的有( )个.
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法:①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF的周长比为1∶2;④△ABC与△DEF的面积比为4∶1. 正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com