
【题目】如图,函数y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0)、(m,0),且1<m<2,下列结论:①abc>0;②0<![]() <
<![]() ;③若点A(﹣3,y1),B(3,y2)在抛物线上,则y1<y2;④a(m﹣1)+b=0.其中结论正确的有( )个.
;③若点A(﹣3,y1),B(3,y2)在抛物线上,则y1<y2;④a(m﹣1)+b=0.其中结论正确的有( )个.
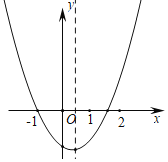
A. 4B. 3C. 2D. 1
【答案】B
【解析】
根据题意画出抛物线的大致图象,利用函数图象,由抛物线开口方向得a>0,由抛物线的对称轴位置得b<0,由抛物线与y轴的交点位置得c<0,于是可对①进行判断;由于抛物线过点(-1,0)和(m,0),且1<m<2,根据抛物线的对称性和对称轴方程得到
0![]() ,则可对②进行判断;利用点A(-3,y1)和点B(3,y2)到对称轴的距离的大小可对进行判断;根据抛物线上点的坐标特征得a-b+c=0,am2+bm+c=0,两式相减得am2-a+bm+b=0,然后把等式左边分解后即可得到a(m-1)+b=0,则可对@进行判断;
,则可对②进行判断;利用点A(-3,y1)和点B(3,y2)到对称轴的距离的大小可对进行判断;根据抛物线上点的坐标特征得a-b+c=0,am2+bm+c=0,两式相减得am2-a+bm+b=0,然后把等式左边分解后即可得到a(m-1)+b=0,则可对@进行判断;
解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在y轴的右侧,
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,
∴①的结论正确;
∵抛物线过点(﹣1,0)和(m,0),且1<m<2,
∴![]() ,故②的结论正确;
,故②的结论正确;
∵点A(﹣3,y1)到对称轴的距离比点B(3,y2)到对称轴的距离远,
∴y1>y2,
∴③的结论错误;
∵抛物线过点(﹣1,0),(m,0),
∴a﹣b+c=0,am2+bm+c=0,
∴am2﹣a+bm+b=0,
a(m+1)(m﹣1)+b(m+1)=0,
∴a(m﹣1)+b=0,
∴④的结论正确;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
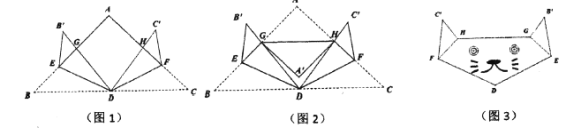
【题目】如图1,在面积为![]() 的等腰
的等腰![]() 纸板中,在直角边
纸板中,在直角边![]() ,
,![]() 上各取一点
上各取一点![]() ,
,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折叠,对应边
折叠,对应边![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,再将
,再将![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点
的对应点![]() 落在
落在![]() 的内部(如图2所示),翻面画上眼睛和鼻子,得到了一幅可爱的“猫脸图”(如图3所示),若点
的内部(如图2所示),翻面画上眼睛和鼻子,得到了一幅可爱的“猫脸图”(如图3所示),若点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() ,则五边形
,则五边形![]() 的面积为__________
的面积为__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
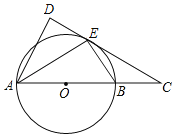
【题目】如图,AB是⊙O的直径,E是⊙O上一点,C在AB的延长线上,AD⊥CE交CE的延长线于点D,且AE平分∠DAC.
(1)求证:CD是⊙O的切线;
(2)若AB=6,∠ABE=60°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OB、OC在∠AOD的内部,下列说法:
①若∠AOC=∠BOD=90°,则与∠BOC互余的角有2个;
②若∠AOD+∠BOC=180°,则∠AOC+∠BOD=180°;
③若OM、ON分别平分∠AOD,∠BOD,则∠MON=![]() ∠AOB;
∠AOB;
④若∠AOD=150°、∠BOC=30°,作∠AOP=![]() ∠AOB、∠DOQ=
∠AOB、∠DOQ=![]() ∠COD,则∠POQ=90°
∠COD,则∠POQ=90°
其中正确的有( )
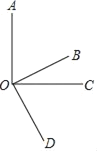
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现需了解2019年各月份中5至14日广州市每天最低气温的情况:图①是3月份的折线统计图.(数据来源于114天气网)
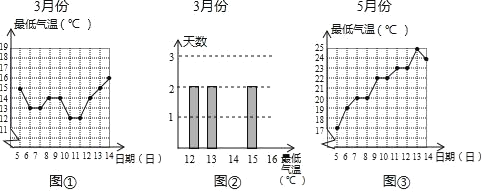
(1)图②是3月份的频数分布直方图,根据图①提供的信息,补全图②中的频数分布直方图;
(2)3月13日与10日这两天的最低气温之差是 ℃;
(3)图③是5月份的折线统计图.用![]() 表示5月份的方差;用
表示5月份的方差;用![]() 表示3月份的方差,比较大小:
表示3月份的方差,比较大小:![]()
![]() ;比较3月份与5月份, 月份的更稳定.
;比较3月份与5月份, 月份的更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣x+1的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分別交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为____________°

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划在暑假第二周的星期一至星期四开展社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择两天,其中有一天是星期二的概率是多少?
(2)乙同学随机选择连续的两天,其中有一天是星期二的概率是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如![]() .善于思考的小明进行了以下探索:
.善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 、
、![]() 、
、![]() 、
、![]() 均为整数),则有
均为整数),则有![]() .
.
![]() ,
,![]() .这样小明就找到了一种把类似
.这样小明就找到了一种把类似![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当![]() 、
、![]() 、
、![]() 、
、![]() 均为正整数时,若
均为正整数时,若![]() ,用含
,用含![]() 、
、![]() 的式子分别表示
的式子分别表示![]() 、
、![]() ,得:
,得:![]() ,
,![]() ;
;
(2)利用所探索的结论,找一组正整数![]() 、
、![]() 、
、![]() 、
、![]() 填空:
填空: ![]()
![]()
![]()
![]()
![]() ;
;
(3)若![]() ,且
,且![]() 、
、![]() 、
、![]() 均为正整数,求
均为正整数,求![]() 的值?
的值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com