
【题目】已知二次函数y=ax2+4x+c,当x=﹣2时,y=﹣5;当x=1时,y=4
(1)求这个二次函数表达式.
(2)此函数图象与x轴交于点A,B(A在B的左边),与y轴交于点C,求点A,B,C点的坐标及△ABC的面积.
(3)该函数值y能否取到﹣6?为什么?
【答案】(1)y=x2+4x﹣1;(2)![]() ;(3)函数值y不能取到﹣6;理由见解析.
;(3)函数值y不能取到﹣6;理由见解析.
【解析】
(1)把x=﹣2时,y=﹣5;x=1时,y=4代入y=ax2+4x+c,求得a、c的值即可求得;
(2)令y=0,解方程求得A、B点的坐标,令x=0,求得y=﹣1,得到C点的坐标,然后根据三角形面积公式即可求得△ABC的面积;
(3)把(1)中求得的解析式化成顶点式,求得函数y的最小值为﹣5,故函数值y不能取到﹣6.
解:(1)把x=﹣2时,y=﹣5;x=1时,y=4代入y=ax2+4x+c得![]() ,
,
解得![]() ,
,
∴这个二次函数表达式为y=x2+4x﹣1;
(2)令y=0,则x2+4x﹣1=0,
解得x=﹣2±![]() ,
,
∴A(﹣2﹣![]() ,0),B(﹣2+
,0),B(﹣2+![]() ,0),
,0),
令x=0,则y=﹣1,
∴C(0,﹣1),
∴△ABC的面积:![]() ABOC=
ABOC=![]() (﹣2+
(﹣2+![]() +2+
+2+![]() )×1=
)×1=![]() ;
;
(3)∵y=x2+4x﹣1=(x+2)2﹣5,
∴函数y的最小值为﹣5,
∴函数值y不能取到﹣6.


科目:初中数学 来源: 题型:
【题目】民俗村的开发和建设带动了旅游业的发展,某市有A、B、C、D、E五个民俗旅游村及“其它”景点,该市旅游部门绘制了2018年“五一”长假期间民俗村旅游情况统计图如下:
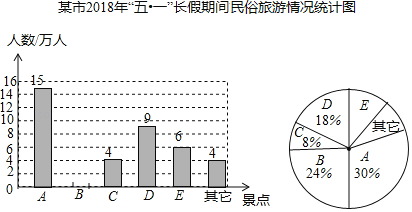
根据以上信息解答:
(1)2018年“五一”期间,该市五个旅游村及“其它”景点共接待游客 万人,扇形统计图中D民俗村所对应的圆心角的度数是 ,并补全条形统计图;
(2)根裾近几年到该市旅游人数增长趋势,预计2019年“五一”节将有70万游客选择该市旅游,请估计有多少万人会选择去E民俗村旅游?
(3)甲、乙两个旅行团在A、C、D三个民俗村中,同时选择去同一个民俗村的概率是多少?请用画树状图或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是2019年4月份的日历,现用一长方形在日历表中任意框出4个数(如图2),下列表示a,b,c,d之间关系的式子中不正确的是( )

A. a﹣d=b﹣cB. a+c+2=b+dC. a+b+14=c+dD. a+d=b+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加2018年的全国初中生数学竞赛,乔老师利用寒假把甲、乙两名同学的前五个学期的数学成绩(单位:分)统计成下表:
第一学期 | 第二学期 | 第三学期 | 第四学期 | 第五学期 | |
甲 | 75 | 80 | 85 | 90 | 95 |
乙 | 95 | 87 | 88 | 80 | 75 |
(1)分别求出甲、乙两名同学前五个学期的数学平均成绩;
(2)在图中分别画出甲、乙两名同学前五个学期的数学成绩的折线统计图;
(3)如果你是乔老师,你认为应该派哪名学生参加数学竞赛?请简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
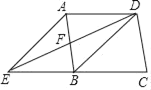
【题目】如图,在平行四边形ABCD中,DB=DA,∠ADB的角平分线与AB相交于点F,与CB的延长线相交于点E连接AE.
(1)求证:四边形AEBD是菱形.
(2)若四边形ABCD是菱形,DC=10,则菱形AEBD的面积是 .(直接填空,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
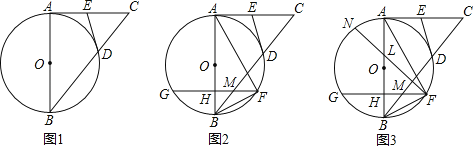
【题目】已知:如图,AB为⊙O的直径,AC与⊙O相切于点A,连接BC交圆于点D,过点D作⊙O的切线交AC于E.
(1)求证:AE=CE
(2)如图,在弧BD上任取一点F连接AF,弦GF与AB交于H,与BC交于M,求证:∠FAB+∠FBM=∠EDC.
(3)如图,在(2)的条件下,当GH=FH,HM=MF时,tan∠ABC=![]() ,DE=
,DE=![]() 时,N为圆上一点,连接FN交AB于L,满足∠NFH+∠CAF=∠AHG,求LN的长.
时,N为圆上一点,连接FN交AB于L,满足∠NFH+∠CAF=∠AHG,求LN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com