
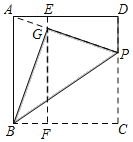
【题目】如图,在一张矩形纸片ABCD中,AB=6cm,点E,F分别是AD和BC的三等分点,现将这张纸片折叠,使点C落在EF上的点G处,折痕为BP.若PG的延长线恰好经过点A,则AD的长为_____cm.
【答案】![]()
【解析】
四根据矩形的性质得到∠C=90°,BC=AD,根据已知条件得到AE=BF=![]() BC,由折叠的性质得到BG=BC,∠BGP=∠C=∠AGB=90°,设BF=x,则BC=BG=3x,解直角三角形即可得到结论.
BC,由折叠的性质得到BG=BC,∠BGP=∠C=∠AGB=90°,设BF=x,则BC=BG=3x,解直角三角形即可得到结论.
∵四边形ABCD是矩形,
∴∠C=90°,BC=AD,
∵点E,F分别是AD和BC的三等分点,
∴AE=BF=![]() BC,
BC,
∴四边形ABFE是矩形,
∴AB∥EF,∠BFE=90°,
∴∠ABG=∠BGF,
∵将这张纸片折叠,使点C落在EF上的点G处,折痕为BP,
∴BG=BC,∠BGP=∠C=∠AGB=90°,
设BF=x,则BC=BG=3x,
∴sin∠BGF=sin∠ABG=![]() ,
,
∵AB=6,
∴AG=![]() AB=2,
AB=2,
∴BG=BC=![]() ,
,
∴AD=BC=![]() ,
,
故答案为![]()


科目:初中数学 来源: 题型:
【题目】费尔兹奖是国际上享有崇高荣誉的一个数学奖项,每4年评选一次,在国际数学家大会上颁给有卓越贡献的年龄不超过40岁的年轻数学家,美籍华人丘成桐1982年获得费尔兹奖.为了让学生了解费尔兹奖得主的年龄情况,我们查取了截止到2018年60名费尔兹奖得主获奖时的年龄数据,并对数据进行整理、描述和分析.下面给出了部分信息.
a.截止到2018年费尔兹奖得主获奖时的年龄数据的频数分布直方图如图1(数据分成5组,各组是28≤x<31,31≤x<34,34≤x<37,37≤x<40,x≥40):
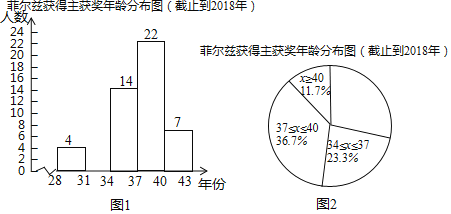
b.如图2,在a的基础上,画出扇形统计图;
c.截止到2018年费尔兹奖得主获奖时的年龄在34≤x<37这一组的数据是:
36 | 35 | 34 | 35 | 35 | 34 | 34 | 35 | 36 | 36 | 36 | 36 | 34 | 35 |
d.截止到2018年时费尔兹奖得主获奖时的年龄的平均数、中位数、众数如下:
年份 | 平均数 | 中位数 | 众数 |
截止到2018 | 35.58 | m | 37,38 |
根据以上信息,回答下列问题:
(1)依据题意,补全频数直方图;
(2)31≤x<34这组的圆心角度数是度,并补全扇形统计图;
(3)统计表中中位数m的值是;
(4)根据以上统计图表试描述费尔兹奖得主获奖时的年龄分布特征.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014湖南怀化)两个城镇A、B与两条公路ME、MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离相等,到两条公路ME、MF的距离也必须相等,且在∠FME的内部.
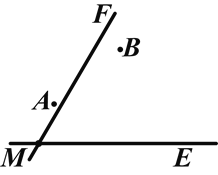
(1)那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C(不写已知、求作、作法,只保留作图痕迹);
(2)设AB的垂直平分线交ME于点N,且![]() km,在M处测得点C位于点M的北偏东60°方向,在N处测得点C位于点N的北偏西45°方向,求点C到公路ME的距离.
km,在M处测得点C位于点M的北偏东60°方向,在N处测得点C位于点N的北偏西45°方向,求点C到公路ME的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发散思维2017·丰台区二模为了解某校八年级学生每周上网的时间,两名学生进行了抽样调查,小丽调查了八年级电脑爱好者中40名学生每周上网的时间,小杰从全校400名八年级学生中随机抽取了40名学生,调查了他们每周上网的时间.小丽与小杰整理各自的样本数据,如下表所示:
时间段(时/周) | 小丽抽样人数 | 小杰抽样人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(表中每组数据包含最小值,不包含最大值)
(1)你认为哪名同学抽取的样本不合理?请说明理由;
(2)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体八年级学生中有多少名学生应适当减少上网的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
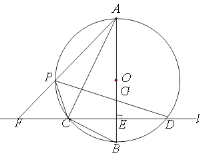
【题目】如图,在⊙O的内接三角形ABC中,![]() ,
,![]() ,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是
,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是![]() 上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
(1)求证:![]() ;
;
(2)若![]() ,
, ![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
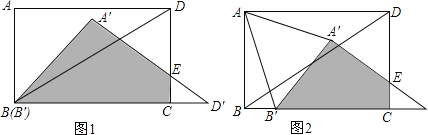
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,连接BD,将△ABD绕B点作顺时针方向旋转得到△A′B′D′(B′与B重合),且点D′刚好落在BC的延长上,A′D′与CD相交于点E.
(1)求矩形ABCD与△A′B′D′重叠部分(如图1中阴影部分A′B′CE)的面积;
(2)将△A′B′D′以每秒2cm的速度沿直线BC向右平移,如图2,当B′移动到C点时停止移动.设矩形ABCD与△A′B′D′重叠部分的面积为y,移动的时间为x,请你直接写出y关于x的函数关系式,并指出自变量x的取值范围;
(3)在(2)的平移过程中,是否存在这样的时间x,使得△AA′B′成为等腰三角形?若存在,请你直接写出对应的x的值,若不存在,请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(x﹣a)(x+5)=x2﹣bx﹣5,一元二次方程ax2+bx+k=0的两个实数根x1,x2满足![]() (x1﹣x2)2﹣2x1x2=4,则k=_____.
(x1﹣x2)2﹣2x1x2=4,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=4![]() ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com