
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作直线DE垂直BC于F,且交BA的延长线于点E.
(1)求证:直线DE是⊙O的切线;
(2)若cos∠BAC= ![]() ,⊙O的半径为6,求线段CD的长.
,⊙O的半径为6,求线段CD的长.
【答案】
(1)
证明:连接BD、OD,
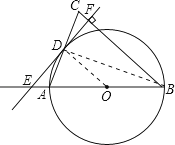
∵AB是⊙O的直径,
∴∠ADB=90°,即BD⊥AC,
∵BA=BC,
∴D为AC中点,又O是AB中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∴∠BFE=∠ODE,
∵DE⊥BC,
∴∠BFE=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴直线DE是⊙O的切线
(2)
解:

∵⊙O的半径为6,
∴AB=12,
在Rt△ABD中,cos∠BAC= ![]() =
= ![]() ,
,
∴AD=4,
由(1)知BD是△ABC的中线,
∴CD=AD=4.
【解析】(1)连接BD、OD,由AB为圆O的直径,利用直径所对的圆周角为直角得到BD与AC垂直,又BA=BC,利用等腰三角形的三线合一性质得到D 为AC的中点,又O为AB的中点,可得出OD为三角形ABC的中位线,利用三角形中位线定理得到OD与BC平行,由EF垂直于BC,得到EF垂直于OD, 可得出EF为圆O的切线;(2)由圆的半径为6,求出直径AB为12,在直角三角形ABD中,由cos∠BAC的值及AB的长,求出AD的长,再由第一问 得到D为AC的中点,得到CD=AD,即可求出CD的长.
【考点精析】本题主要考查了圆周角定理和切线的判定定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:
【题目】如图,根据2013﹣2017年某市财政总收入(单位:亿元)统计图所提供的信息,下列判断正确的是( )
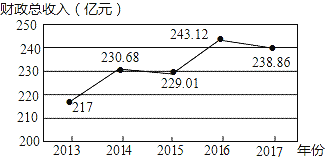
A. 2013~2017年财政总收入呈逐年增长
B. 预计2018年的财政总收入约为253.43亿元
C. 2014~2015年与2016~2017年的财政总收入下降率相同
D. 2013~2014年的财政总收入增长率约为6.3%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数
的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数![]() 的图象上,点D的坐标为
的图象上,点D的坐标为![]() .将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上.
.将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A1B1B2C1 , A2B2B3C2 , A3B3B4C3 , …,AnBnBn+1Cn , 按如图所示放置,使点A1、A2、A3、A4、…、An在射线OA上,点B1、B2、B3、B4、…、Bn在射线OB上.若∠AOB=45°,OB1=1,图中阴影部分三角形的面积由小到大依次记作S1 , S2 , S3 , …,Sn , 则Sn= . 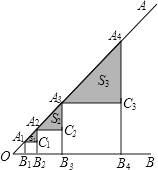
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“端午节”期间,小明、小亮等同学随家长一行共12人到某公园游玩,成人门票每张40元,学生门票5折优惠,小明直接去窗口买票需要400元.
(1)他们共去了几个成人,几个学生?
(2)小亮从美团网看到订团体票信息,9人以上(含9人)的团体订票按成人价8.5折优惠,请你帮助策划,用何种方式购票最省钱,给出方案并计算出票价总数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由; 
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com