
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由; 
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
【答案】
(1)
解:由抛物线y=ax2+bx+2过点A(﹣3,0),B(1,0),则
![]()
解这个方程组,得a=﹣ ![]() ,b=﹣
,b=﹣ ![]() .
.
∴二次函数的关系解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)
解:设点P坐标为(m,n),则n=﹣ ![]() m2﹣
m2﹣ ![]() m+2.
m+2.
连接PO,作PM⊥x轴于M,PN⊥y轴于N.
PM=﹣ ![]() m2﹣
m2﹣ ![]() m+2,PN=﹣m,AO=3.
m+2,PN=﹣m,AO=3.
当x=0时,y=﹣ ![]() ×0﹣
×0﹣ ![]() ×0+2=2,所以OC=2
×0+2=2,所以OC=2
S△PAC=S△PAO+S△PCO﹣S△ACO
= ![]() AOPM+
AOPM+ ![]() COPN﹣
COPN﹣ ![]() AOCO
AOCO
= ![]() ×3(﹣
×3(﹣ ![]() m2﹣
m2﹣ ![]() m+2)+
m+2)+ ![]() ×2(﹣m)﹣
×2(﹣m)﹣ ![]() ×3×2
×3×2
=﹣m2﹣3m
∵a=﹣1<0
∴函数S△PAC=﹣m2﹣3m有最大值
当m=﹣ ![]() =﹣
=﹣ ![]() 时,S△PAC有最大值.
时,S△PAC有最大值.
此时n=﹣ ![]() m2﹣
m2﹣ ![]() m+2=﹣
m+2=﹣ ![]() =
= ![]()
∴存在点P(﹣ ![]() ,
, ![]() ),使△PAC的面积最大
),使△PAC的面积最大
(3)
解:如图(3)所示,
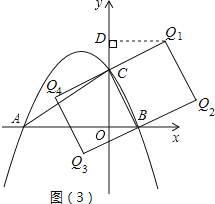
以BC为边在两侧作正方形BCQ1Q2、正方形BCQ4Q3,则点Q1,Q2,Q3,Q4为符合题意要求的点.
过Q1点作Q1D⊥y轴于点D,
∵∠BCQ1=90°,
∴∠Q1CD+∠OCB=90°,
又∵在直角△OBC中,∠OCB+∠CBO=90°,
∴∠Q1CD=∠OCB,
又∵Q1C=BC,∠Q1DC=∠BOC,
∴△Q1CD≌△CBO,
∴Q1D=OC=2,CD=OB=1,∴OD=OC+CD=3,∴Q1(2,3);
同理求得Q2(3,1),Q3(﹣1,﹣1),Q4(﹣2,1).
∴存在点Q,使△BCQ是以BC为腰的等腰直角三角形.Q点坐标为:Q1(2,3),Q2(3,1),Q3(﹣1,﹣1),Q4(﹣2,1)
(4)
解:如图(4)所示,
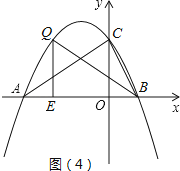
设E(n,0),则BE=1﹣n,QE=﹣ ![]() n2﹣
n2﹣ ![]() n+2.
n+2.
假设以点B、Q、E为顶点的三角形与△AOC相似,则有两种情况:
①若△AOC∽△BEQ,则有: ![]() ,
,
即 ![]() ,化简得:n2+n﹣2=0,
,化简得:n2+n﹣2=0,
解得n1=﹣2,n2=1(与B重合,舍去),∴n=﹣2,QE=﹣ ![]() n2﹣
n2﹣ ![]() n+2=2.
n+2=2.
∴Q(﹣2,2);
②若△AOC∽△BQE,则有: ![]() ,
,
即 ![]() ,化简得:4n2﹣n﹣3=0,
,化简得:4n2﹣n﹣3=0,
解得n1=﹣ ![]() ,n2=1(与B重合,舍去),∴n=﹣
,n2=1(与B重合,舍去),∴n=﹣ ![]() ,QE=﹣
,QE=﹣ ![]() n2﹣
n2﹣ ![]() n+2=
n+2= ![]() .
.
∴Q(﹣ ![]() ,
, ![]() ).
).
综上所述,存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似.
Q点坐标为(﹣2,2)或(﹣ ![]() ,
, ![]() )
)
(5)
解:假设存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形.①若CM平行于x轴,如图(5)a所示, 
有符合要求的两个点Q1,Q2,此时Q1A=Q2A=CM.
∵CM∥x轴,∴点M、点C(0,2)关于对称轴x=﹣1对称,
∴M(﹣2,2),∴CM=2.
由Q1A=Q2A=CM=2,得到Q1(﹣5,0),Q2(﹣1,0);
②若CM不平行于x轴,如图(5)b所示.

过点M作MG⊥x轴于G,
易证△MGQ≌△COA,得QG=OA=3,MG=OC=2,即yM=﹣2.
设M(x,﹣2),则有﹣ ![]() x2﹣
x2﹣ ![]() x+2=﹣2,解得x=﹣1±
x+2=﹣2,解得x=﹣1± ![]() .
.
又QG=3,∴xQ=xG+3=2± ![]() ,
,
∴Q3(2+ ![]() ,0),Q4(2﹣
,0),Q4(2﹣ ![]() ,0).
,0).
综上所述,存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形.Q点坐标为:Q1(﹣5,0),Q2(﹣1,0),Q3(2+ ![]() ,0),Q4(2﹣
,0),Q4(2﹣ ![]() ,0).
,0).
【解析】(1)利用待定系数法求出抛物线的解析式;(2)关键是求出△ACP面积的表达式,然后利用二次函数求极值的方法,求出△ACP面积的最大值;(3)如图(3)所示,以BC为边,在线段BC两侧分别作正方形,正方形的其他四个顶点均可以使得“△BCQ是以BC为腰的等腰直角三角形”,因此有四个点符合题意要求;(4)如图(4)所示,若以点B、Q、E为顶点的三角形与△AOC相似,有两种情况,需要分类讨论,不要漏解;(5)以A、C、M、Q为顶点的四边形是平行四边形,有四种情况,分别如图(5)a、图(5)b所示,注意不要漏解.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作直线DE垂直BC于F,且交BA的延长线于点E.
(1)求证:直线DE是⊙O的切线;
(2)若cos∠BAC= ![]() ,⊙O的半径为6,求线段CD的长.
,⊙O的半径为6,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,其中A(1,1),B(3,1),D(1,3).反比例函数 ![]() 的图象经过对角线BD的中点M,与BC,CD的边分别交于点P、Q.
的图象经过对角线BD的中点M,与BC,CD的边分别交于点P、Q.
(1)直接写出点M,C的坐标;
(2)求直线BD的解析式;
(3)线段PQ与BD是否平行?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() 平分
平分![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() .
.
【1】求![]() 的度数
的度数
【2】如图②,若把“![]() ⊥
⊥![]() ”变成“点F在DA的延长线上,
”变成“点F在DA的延长线上,![]() ”,其它条件不变,求
”,其它条件不变,求![]() 的度数;
的度数;
【3】如图③,若把“![]() ⊥
⊥![]() ”变成“
”变成“![]() 平分
平分![]() ”,其它条件不变,
”,其它条件不变,![]() 的大小是否变化,并请说明理由.(此题9分)
的大小是否变化,并请说明理由.(此题9分)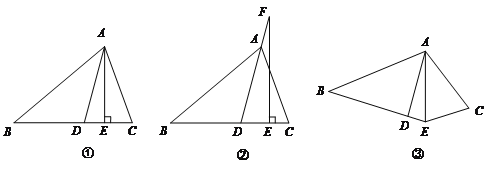
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东方红中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向西走100米到聪聪家,再向东走150米到青青家,再向西走200米到刚刚家,请问:
(1)如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出聪聪家与青青家的大概位置(数轴上一格表示50米).
(2)聪聪家与刚刚家相距多远?
(3)聪聪家向西20米所表示的数是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有若干个数,第一个数记为a1,第二个数记为a2,第三个数记为a3,…,第n个数记为an,若a1=![]() ,从第二个数起,每个数都等于“1与它前面那个数差的倒数”.
,从第二个数起,每个数都等于“1与它前面那个数差的倒数”.
(1)计算:a2 ,a3 ,a4 ,a5的值;
(2)这排数有什么规律?由你发现的规律,计算a2014的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=﹣ ![]() x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA. 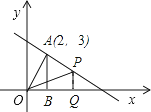
(1)求此一次函数的解析式;
(2)设点P为直线y=﹣ ![]() x+b上的一点,且在第一象限内,经过P作x轴的垂线,垂足为Q.若S△POQ=
x+b上的一点,且在第一象限内,经过P作x轴的垂线,垂足为Q.若S△POQ= ![]() S△AOB , 求点P的坐标.
S△AOB , 求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
①abc<0;②a(b+c)>0;③a﹣c=b;④![]() .
.
![]()
其中正确的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com