
分析 (1)分段讨论当100<x≤200和当200<x≤300的函数关系式,
(2)由年获利=年销售额-生产成本-节电投资分别列出当100<x≤200和200<x≤300的利润关系式,求出最大利润,
(3)依题意可知,当100<x≤200时,写出第二年w与x关系为式,由第二年的盈利为1842万元,解得单价x.
解答 解:(1)当100<x≤200时,
y=20-$\frac{x-100}{10}$×0.8
=-0.08x+28,
可见x=200元时,y=28-16=12(万件)
当200<x≤300时,
y=12-$\frac{x-200}{10}$×1=-0.1x+32;
(2)投资成本为480+1520=2000万元
y=-0.08x+28,100≤x<200,
w=xy-40y-2000
=(x-40)(-0.08x+28)-2000
=-0.08x2+31.2x-3120
=-0.08(x-195)2-78
可见第一年在100≤x<200注定亏损,x=195时亏损最少,为78万元
200≤x≤300,y=-0.1x+32,
w=xy-40y-2000
=(x-40)(-0.1x+32)-2000
=-0.1x2+36x-3280
=-0.1(x-180)2-40
可见第一年在200≤x≤300注定亏损,x=200时亏损最少,为80万元
综上可见,x=195时亏损最少,为78万元.
(3)依题意可知,当100<x≤200时,第二年w与x之间的函数关系为
w=(x-40)(-0.08x+28)-78,
当总利润刚好为1842万元时,依题意得(x-40)(-0.08x+28)-78=1842
整理,得x2-390x+38000=0,
解得,x1=190,x2=200
答:要使产品销售量最大,销售单价应定为190元或200元.
点评 本题主要考查了二次函数在实际中应用,最大销售利润的问题常利函数的增减性来解答,我们首先要弄懂题意,确定变量,建立函数模型解答,其中要注意应该在自变量的取值范围内求最大值.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
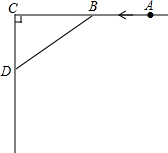 如图,AC⊥CD,甲、乙两人分别骑自行车从相距10km的A,C两地同时出发,各沿箭头所指方向前进.已知甲的速度是16km/h,乙的速度是12km/h,且当甲到达C地时两人停止运动.问:出发多少时间后两人相距最近?最近距离为多少千米?
如图,AC⊥CD,甲、乙两人分别骑自行车从相距10km的A,C两地同时出发,各沿箭头所指方向前进.已知甲的速度是16km/h,乙的速度是12km/h,且当甲到达C地时两人停止运动.问:出发多少时间后两人相距最近?最近距离为多少千米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{27}$ | C. | $\sqrt{8}$ | D. | $\sqrt{75}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
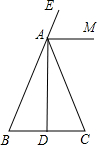 如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.
如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
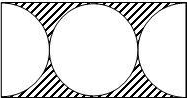 如图,长方形中有两个半圆和一个圆,一直长方形宽为a,则阴影部分的面积为( )
如图,长方形中有两个半圆和一个圆,一直长方形宽为a,则阴影部分的面积为( )| A. | (2-π)a2 | B. | (2-$\frac{π}{4}$)a2 | C. | (2-$\frac{π}{2}$)a2 | D. | (1-$\frac{π}{4}$)a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 1或-1 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com