Question

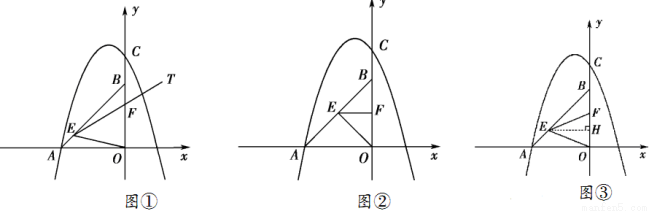
如图，在平面直角坐标系中，点A坐标为(-2，0)，点B坐标为（0，2），点E为线段AB上的动点(点E不与点A，B重合)，以E为顶点作∠OET=45°，射线ET交线段OB于点F，C为y轴正半轴上一点，且OC=AB，抛物线y=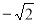x2+mx+n的图象经过A，C两点.

（1）求此抛物线的函数表达式；

（2）求证：∠BEF=∠AOE；

（3）当△EOF为等腰三角形时，求此时点E的坐标；

（4）在（3）的条件下，当直线EF交x轴于点D，P为（1）中抛物线上一动点，直线PE交x轴于点G，在直线EF上方的抛物线上是否存在一点P，使得△EPF的面积是△EDG面积的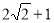（）倍.若存在，请直接写出点P坐标；若不存在，请说明理由．

 

Answer 1

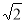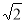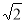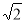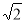（1）y=-x2-x+2；（2）证明见解析；（3）(-1， 1)，(-， 2-)；（4）P(0， 2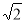)或P（-1，2）

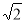【解析】

试题分析：（1）首先求出点C的坐标，然后利用待定系数法求出抛物线的解析式；

（2）利用三角形外角性质，易证∠BEF=∠AOE；

（3）当△EOF为等腰三角形时，有三种情况，需要分类讨论，注意不要漏解；

（4）本问关键是利用已知条件求得点P的纵坐标，要点是将△EPF与△EDG的面积之比转化为线段之比．如图④所示，首先证明点E为DF的中点，然后作x轴的平行线FN，则△EDG≌△EFN，从而将△EPF与△EDG的面积之比转化为PE：NE；过点P作x轴垂线，可依次求出线段PT、PM的长度，从而求得点P的纵坐标；最后解一元二次方程，确定点P的坐标．

试题解析：（1） 如答图①， ∵A（-2，0）B（0，2）

∴OA=OB=2 ∴AB2=OA2+OB2=22+22=8∴AB=2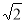∵OC=AB∴OC=2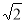， 即C （0，2）

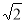又∵抛物线y=-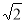x2+mx+n的图象经过A、C两点 则可得解得：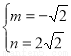

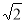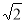∴抛物线的表达式为y=-x2-x+2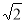

（2） ∵OA=OB ∠AOB=90° ∴∠BAO=∠ABO=45°

又∵∠BEO=∠BAO+∠AOE=45°+∠AOE

∠BEO=∠OEF+∠BEF=45°+∠BEF ∴∠BEF=∠AOE

（3） 当△EOF为等腰三角形时，分三种情况讨论

①当OE=OF时， ∠OFE=∠OEF=45°

在△EOF中， ∠EOF=180°-∠OEF-∠OFE=180°-45°-45°=90°

又∵∠AOB＝90°

则此时点E与点A重合， 不符合题意， 此种情况不成立.

②如答图②， 当FE=FO时，

∠EOF=∠OEF=45°

在△EOF中，∠EFO=180°-∠OEF-∠EOF=180°-45°-45°=90°

∴∠AOF+∠EFO=90°+90°=180°∴EF∥AO ∴ ∠BEF=∠BAO=45° 又∵ 由 (2) 可知 ，∠ABO=45°∴∠BEF=∠ABO ∴BF=EF∴EF=BF=OF=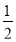OB=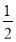×2＝1 ∴ E(-1， 1)

③如答图③， 当EO=EF时， 过点E作EH⊥y轴于点H 在△AOE和△BEF中，

∠EAO=∠FBE， EO=EF， ∠AOE=∠BEF ∴△AOE≌△BEF ∴BE=AO=2

∵EH⊥OB ∴∠EHB=90°∴∠AOB=∠EHB ∴EH∥AO ∴∠BEH=∠BAO=45°

在Rt△BEH中， ∵∠BEH=∠ABO=45° ∴EH=BH=BEcos45°=2×=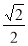

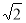
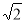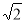∴OH=OB-BH=2- ∴ E(-， 2-)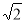

综上所述， 当△EOF为等腰三角形时， 所求E点坐标为E(-1， 1)或E(-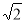， 2- )

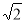（4） P(0， 2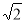)或P （-1， 2 ）

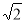考点: 二次函数综合题．