
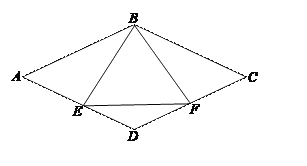
【题目】如图,已知四边形ABCD是菱形,点E、F分别是菱形ABCD边AD、CD的中点.
(1)求证:BE=BF;
(2)当△BEF为等边三角形时,求![]() 的度数.
的度数.
【答案】(1)证明见解析(2)120°
【解析】分析:(1)利用菱形的性质证明△ABE≌△BCF,即可证出BE=BF;
(2)取BF的中点G,连接EG,先证四边形ABFD是梯形,再证EG是梯形ABFD的中位线,即可得到∠ABF=90°,进而可求出![]() 的度数.
的度数.
详解:(1)证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠A=∠C
∵点E、F分别为菱形ABCD边AD、CD的中点.
∴AE=CF ,
又∵ ∠A=∠C,AB=BC,
∴△ABE≌△BCF,
∴BE=BF;
(2) 取BF的中点G,连接EG,
∵△BEF为等边三角形,
∴EG⊥BF,
∵四边形ABCD是菱形,
∴AB∥DF,
又∵AD与BF不平行,
∴四边形ABFD是梯形
∵E是AD中点,G是BF的中点,
∴EG是梯形ABFD的中位线,
∴EG∥AB,
∵EG⊥BF,
∴AB⊥BF,
∴∠ABF=90°,
∵△BEF为等边三角形,
∴∠EBF=60°,
∴∠ABE=30° ,
∵△ABE≌△BCF,
∴∠ABE=∠CBF= 30°,
∴∠ABC=120°.


科目:初中数学 来源: 题型:
【题目】计算:
(1) (2![]() -3
-3![]() )÷
)÷![]() ; (2) (
; (2) (![]() -
-![]() )2+2
)2+2![]() ×
×![]() ;
;
(3) ![]() ; (4) (
; (4) (![]() -2
-2![]() )×
)×![]() -4
-4![]() ;
;
(5)(![]() -1)(
-1)(![]() +1)-(-
+1)-(-![]() )-2+|1-
)-2+|1-![]() |-(π-2)0+
|-(π-2)0+![]() ;
;
(6)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费 ![]() 元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
月份 | 用水量x(吨) | 水费y(元) |
四月 | 35 | 59.5 |
五月 | 80 | 151 |

(1)求出m的值;
(2)写出y与x之间的函数关系式,并指出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC,四块阴影部分的面积分别为S1、S2、S3、S4.则S1+S2+S3+S4等于( )
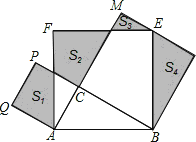
A.14 B.16 C.18 D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照有关规定:距离铁轨道200米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.
如图是一个小区平面示意图,矩形ABEF为一新建小区,直线MN为高铁轨道,C、D是直线MN上的两点,点C、A、B在一直线上,且DA⊥CA,∠ACD=30°.小王看中了①号楼A单元的一套住宅,与售楼人员的对话如下:

(1)小王心中一算,发现售楼人员的话不可信,请你通过计算用所学的数学知识说明理由.
(2)若一列长度为228米的高铁以70米/秒的速度通过时,则A单元用户受到影响时间有多长?( 温馨提示:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈6.1)
≈6.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)3ab2(﹣![]() a2b)2abc;
a2b)2abc;
(2)(﹣![]() x2y)3(﹣3xy2);
x2y)3(﹣3xy2);
(3)(﹣3xy2)3(![]() x3y);
x3y);
(4)(x2+3x)﹣2(4x﹣x2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长. (参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com