
 如图,在四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26,求四边形ABCD的面积.
如图,在四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26,求四边形ABCD的面积. 分析 先根据勾股定理求出AC的长,在根据勾股定理的逆定理推出△ACB也是直角三角形,然后将两个直角三角形的面积相加即可.
解答 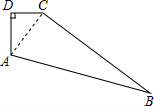 解:连接AC,
解:连接AC,
∵在Rt△ADC中,∠D=90°,CD=6,AD=8,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{100}$=10,
又因为在△ACB中,AB2=262=676,
AC2+BC2=102+576=676,
∴AB2=AC2+BC2,
∴△ACB也是直角三角形.
∴四边形ABCD的面积等于S△ADC+S△ACB,
即$\frac{1}{2}$AD•DC+$\frac{1}{2}$AC•BC=$\frac{1}{2}$×6×8+$\frac{1}{2}$×10×24=144.
答:四边形ABCD的面积为144.
点评 此题主要考查了勾股定理和勾股定理的逆定理的理解和掌握,解答此题的关键是利用勾股定理的逆定理推出△ACB也是直角三角形,然后即可得出答案了.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠C=90°,AC=3cm,BC=6cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从C出发以1cm/s的速度向点A移动,如果动点P、Q同时出发,要使△CBA与C、P、Q三点构成的三角形相似,求所需要的时间是多少秒?
如图,△ABC中,∠C=90°,AC=3cm,BC=6cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从C出发以1cm/s的速度向点A移动,如果动点P、Q同时出发,要使△CBA与C、P、Q三点构成的三角形相似,求所需要的时间是多少秒?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD中,M为AD边上的一点,连接BM,过C点作CN∥BM,交AD的延长线于点N,在CN上截取CE=BC,连接BE交CD于F.
如图,正方形ABCD中,M为AD边上的一点,连接BM,过C点作CN∥BM,交AD的延长线于点N,在CN上截取CE=BC,连接BE交CD于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=-3}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某农民带了若干千克土豆进城出售,为了方便,他带了一些零用钱备用,他先按市场价卖出一些后,又降价卖,卖出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示.结合图象回答下列问题:
某农民带了若干千克土豆进城出售,为了方便,他带了一些零用钱备用,他先按市场价卖出一些后,又降价卖,卖出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示.结合图象回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com