
【题目】如图1,四边形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求四边形![]() 的面积;
的面积;
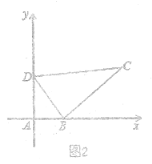
(2)如图2,以![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴建立直角坐标系,点
轴建立直角坐标系,点![]() 在
在![]() 轴上,若
轴上,若![]() ,求
,求![]() 的坐标.
的坐标.
【答案】(1)36;(2)(0,0)或(0,8)
【解析】
(1)连接BD,根据勾股定理可以求得BD的长,然后根据勾股定理的逆定理可以判断△BDC的形状,从而可以解答本题;
(2)先根据![]() ,求出PD的长度,再根据D点的坐标即可求解.
,求出PD的长度,再根据D点的坐标即可求解.
解:(1)连接BD,
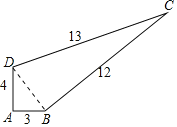
∵在△ABD中,∠DAB=90°,
∴BD2=AB2+AD2=32+42=25,
∴BD=5,
∵在△DBC中,DB2+BC2=52+122=25+144=169,CD2=132=169,
∴DB2+BC2=CD2,
∴△DBC是直角三角形,
∴∠DBC=90°,
∴S四边形ABCD=S△DAB+S△DBC=![]() ×3×4+
×3×4+![]() ×5×12=36.
×5×12=36.
(2)∵S△PBD=![]() S四边形ABCD,
S四边形ABCD,
∴![]() PDAB=
PDAB=![]() ×36=6,
×36=6,
∴![]() PD×3=6,
PD×3=6,
∴PD=4,
∵D(0,4),点P在y轴上,
∴P的坐标为(0,0)或(0,8).


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】类比转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
(1)尝试探究
如图(1),在正方形ABCD中,对角线AC、BD相交于点O,点E是BC边上一点,AE与BD交于点G,过点E作EF⊥AE交AC于点F,若![]() =2,则
=2,则![]() 的值是 ;
的值是 ;
(2)拓展迁移
如图(2),在矩形ABCD中,过点B作BH⊥AC于点O,交AD相于点H,点E是BC边上一点,AE与BH相交于点G,过点E作EF⊥AE交AC于点F.
①若∠BAE=∠ACB,sin∠EAF=![]() ,求tan∠ACB;
,求tan∠ACB;
②若![]() ,
,![]() =b(a>0,b>0),求
=b(a>0,b>0),求![]() 的值(用含a,b的代数式表示).
的值(用含a,b的代数式表示).
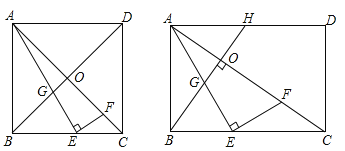
图(1) 图(2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将下列事件发生的概率标在图中:
(1)从高处抛出的物体必落到地面;
(2)从装有![]() 个红球的袋子中任取一个,取出的球是白球;
个红球的袋子中任取一个,取出的球是白球;
(3)月亮绕着地球转;
(4)从装有![]() 个红球、
个红球、![]() 个白球的口袋中任取一个球,恰好是红球(这些球除颜色外完全相同);
个白球的口袋中任取一个球,恰好是红球(这些球除颜色外完全相同);
(5)三名选手抽签决定比赛顺序(有三个签,分别写有![]() ,
,![]() ,
,![]() ),抽到写有
),抽到写有![]() 的签.
的签.
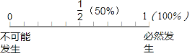
查看答案和解析>>
科目:初中数学 来源: 题型:
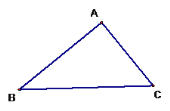
【题目】如图,三个村庄A、B、C之间的距离分别为AB=12km,AC=5km,BC=13km,要从A修一条公路AD直达BC,已知公路的造价为26000元/km,求这条公路的最低造价是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
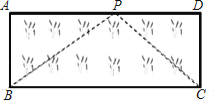
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边的中点,DE⊥BC交AB于点E,AD=AC,EC交AD于点F.
(1)求证:△ABC∽△FCD;
(2)求证:FC=3EF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com