
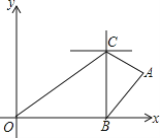
【题目】如图,正方形![]() 的边长为5,
的边长为5,![]() ,
,![]() ,连接
,连接![]() ,则线段
,则线段![]() 的长为( )
的长为( )
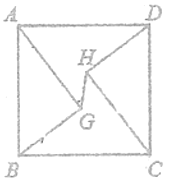
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
延长BG交CH于点E,根据正方形的性质证明△ABG≌△CDH≌△BCE,可得GE=BE-BG=1,HE=CH-CE=1,∠HEG=90°,由勾股定理可得GH的长.
解:如图,延长BG交CH于点E,
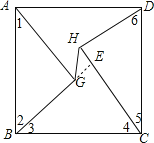
在△ABG和△CDH中,
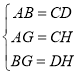 ,
,
∴△ABG≌△CDH(SSS),
AG2+BG2=AB2,
∴∠1=∠5,∠2=∠6,∠AGB=∠CHD=90°,
∴∠1+∠2=90°,∠5+∠6=90°,
又∵∠2+∠3=90°,∠4+∠5=90°,
∴∠1=∠3=∠5,∠2=∠4=∠6,
在△ABG和△BCE中,
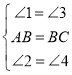 ,
,
∴△ABG≌△BCE(ASA),
∴BE=AG=4,CE=BG=3,∠BEC=∠AGB=90°,
∴GE=BE![]() BG=4-3=1,
BG=4-3=1,
同理可得:HE=1,
在Rt△GHE中,GH=![]() ,
,
故选:C.


科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为![]() 、
、![]() 、
、![]() ,(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为
,(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为![]() 的圆形区域(只考虑在海平面上的探测).
的圆形区域(只考虑在海平面上的探测).
(1)若在三艘海监船组成的![]() 区域内没有探测盲点,则雷达的有效探测半径
区域内没有探测盲点,则雷达的有效探测半径![]() 至少为________海里;
至少为________海里;
(2)某时刻海面上出现一艘菲律宾海警船![]() ,在海监船
,在海监船![]() 测得点
测得点![]() 位于南偏东
位于南偏东![]() 方向上,同时在海监船
方向上,同时在海监船![]() 测得
测得![]() 位于北偏东
位于北偏东![]() 方向上,海警船
方向上,海警船![]() 正以每小时
正以每小时![]() 海里的速度向正西方向移动,我海监船
海里的速度向正西方向移动,我海监船![]() 立刻向北偏东
立刻向北偏东![]() 方向运动进行拦截,问我海监船
方向运动进行拦截,问我海监船![]() 至少以多少速度才能在此方向上拦截到菲律宾海警船
至少以多少速度才能在此方向上拦截到菲律宾海警船![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】聪聪参加我市电视台组织的“阳光杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有![]() 个选项,第二道单选题有4个选项,这两道题聪聪都不会,不过聪聪还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
个选项,第二道单选题有4个选项,这两道题聪聪都不会,不过聪聪还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果聪聪两次“求助”都在第一道题中使用,那么聪聪通关的概率是 .
(2)如果聪聪将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
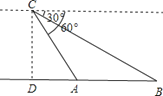
查看答案和解析>>
科目:初中数学 来源: 题型:
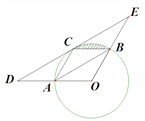
【题目】如图,□AOBC的顶点A、B、C在⊙O上,过点C作DE∥AB交OA延长线于D点,交OB延长线于点E .
(1)求证:CE是⊙O的切线;
(2)若OA=1,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD.
(1)求证:△COD 是等边三角形.
(2)求∠OAD 的度数.
(3)探究:当α为多少度时,△AOD 是等腰三角形?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com