练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

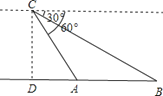
    【题目】某日，正在我国南海海域作业的一艘大型渔船突然发生险情，相关部门接到求救信号后，立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援．当飞机到达距离海面3000米的高空C处，测得A处渔政船的俯角为60°，测得B处发生险情渔船的俯角为30°，请问：此时渔政船和渔船相距多远？（结果保留根号）

    【答案】2000米．

    【解析】

    试题在Rt△CDB中求出BD，在Rt△CDA中求出AD，继而可得AB，即此时渔政船和渔船的距离．

    试题解析：在Rt△CDA中，∠ACD=30°，CD=3000米， ∴AD=CDtan∠ACD=1000米，

    在Rt△CDB中，∠BCD=60°， ∴BD=CDtan∠BCD=3000米， ∴AB=BD﹣AD=2000米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，各边长为 2 的等边三角形有一条 边在同一条直线上，设△B2D1C1 面 积为 S1，△B3D2C2 的面积为 S2，…，△B2019D2018C2018 的面积为 S2018，则 S2018=（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小聪和小明沿同一条路同时从学校出发到学校图书馆查阅资料，学校与图书馆的路程是千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达图书馆，图中折线和线段分别表示两人离学校的路程（千米）与所经过的时间（分钟）之间的函数关系，请根据图象回答下列问题：

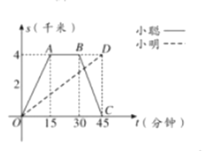
    （1）小聪在图书馆查阅资料的时间为 分钟，小聪返回学校的速度为 千米/分钟；

    （2）请你求出小明离开学校的路程（千米）与所经过的时间（分钟）之间的函数关系；

    （3）求线段的函数关系式；

    （4）当小聪与小明迎面相遇时，他们离学校的路程是多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从宁海县到某市，可乘坐普通列车或高铁，已知高铁的行驶路程与普通列车的行驶路程之和是920千米，而普通列车的行驶路程是高铁的行驶路程的1.3倍．

    （1）求普通列车的行驶路程；

    （2）若高铁的平均速度（千米/时）是普通列车的平均速度（千米/时）的2.5倍，且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时，求高铁的平均速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与实践

    问题发现

    如图，中，平分，平分，经过点，与、相交于点、，且．

    求证：的周长等于．

    （1）小明做完该题后，发现、、存在特定的数量关系，请你直接写出这个数量关系；

    拓广探索

    （2）如图1，将题中“平分”改为“平分的外角”，其他条件不变，请判断、、的数量关系，并证明这个数量关系；

    （3）如图2，将题中“平分，平分”改为“平分的外角，平分的外角”，其他条件不变，请直接写出、、的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数（a≠0）的图象交x轴于A、B两点，交y轴于点D，点B的坐标为（3，0），顶点C的坐标为（1，4）．

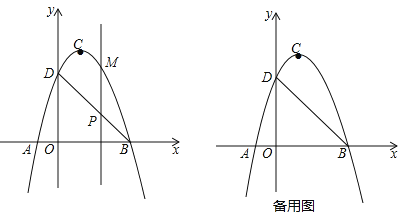
    （1）求二次函数的解析式和直线BD的解析式；

    （2）点P是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M，当点P在第一象限时，求线段PM长度的最大值；

    （3）在抛物线上是否存在异于B、D的点Q，使△BDQ中BD边上的高为？若存在求出点Q的坐标；若不存在请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图①，在平行四边形ABCD中，AB=3cm，BC=5cm，AC⊥AB．△ACD沿AC的方向匀速平移得到△PNM，速度为1cm/s；同时，点Q从点C出发，沿着CB方向匀速移动，速度为1cm/s；当△PNM停止平移时，点Q也停止移动，如图②．设移动时间为t（s）（0＜t＜4）．连接PQ、MQ、MC．解答下列问题：

    （1）当t为何值时，PQ∥AB？

    （2）当t=3时，求△QMC的面积；

    （3）是否存在某一时刻t，使PQ⊥MQ？若存在，求出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：河上有一座抛物线形桥洞，已知桥下的水面离桥拱顶部3m时，水面宽AB＝6m，建立如图所示的坐标系．

    （1）当水位上升0.5m时，求水面宽度CD为多少米？（结果可保留根号）

    （2）有一艘游船它的左右两边缘最宽处有一个长方体形状的遮阳棚，此船正对着桥洞在上述河流中航行，若这船宽（最大宽度）2米，从水面到棚顶高度为1.8米．问这艘船能否从桥下洞通过？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在半径为2cm，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则图中阴影部分的面积为_____．

    查看答案和解析>>

    同步练习册答案