
【题目】已知在△ABC中,∠BAC=![]() ,∠ABC=
,∠ABC=![]() ,∠BCA=
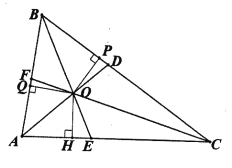
,∠BCA=![]() ,△ABC的三条角平分线AD,BE,CF交于点O,过O向△ABC三边作垂线,垂足分别为P,Q,H,如下图所示。
,△ABC的三条角平分线AD,BE,CF交于点O,过O向△ABC三边作垂线,垂足分别为P,Q,H,如下图所示。
(1)若![]() =78°,
=78°,![]() =56°,
=56°,![]() =46°,求∠EOH的大小;
=46°,求∠EOH的大小;
(2)用![]() ,
,![]() ,
,![]() 表示∠EOH的表达式为∠EOH= ;(要求表达式最简)
表示∠EOH的表达式为∠EOH= ;(要求表达式最简)
(3)若![]() ≥
≥![]() ≥
≥![]() ,∠EOH+∠DOP+∠FOQ=
,∠EOH+∠DOP+∠FOQ=![]() ,判断△ABC的形状并说明理由。
,判断△ABC的形状并说明理由。
【答案】(1)16°;(2)∠EOH=![]() +
+![]()
![]() -90°;(3)△ABC是直角三角形,理由见解析。
-90°;(3)△ABC是直角三角形,理由见解析。
【解析】
(1)由角平分线的性质求出∠EBA,再根据三角形内角和定理可知∠BEA,在Rt△OHE中可求得∠EOH的大小;
根据(1)中过程可表示;
由(2)同理可用![]() ,
,![]() ,
,![]() 表示∠DOP和∠FOQ,将∠EOH+∠DOP+∠FOQ=
表示∠DOP和∠FOQ,将∠EOH+∠DOP+∠FOQ=![]() 中的∠EOH,∠DOP和∠FOQ进行等量代换,可得出
中的∠EOH,∠DOP和∠FOQ进行等量代换,可得出![]() ,
,![]() ,
,![]() 间的关系,由此可判断△ABC的形状.
间的关系,由此可判断△ABC的形状.
解(1)∵BE平分∠ABC(已知) ∠ABC=![]() (已知)
(已知)
∴∠EBA=![]() ∠ABC=
∠ABC=![]()
![]() (角平分线性质)
(角平分线性质)
∵∠BAC=![]() (已知)
(已知)
∴∠BEA=180°-∠BAC-∠EBA=180°-![]() -
-![]()
![]() (三角形内角和180°)
(三角形内角和180°)
∵OH⊥AC(已知)
∴∠OHE=90°(垂直的定义)
∴在Rt△OHE中,∠EOH=90°-∠OEH=90-∠BEA=90-(180°-![]() -
-![]()
![]() )=16°
)=16°
(2) 由(1)知 ∠EOH=![]() +
+![]()
![]() -90°
-90°
(3) 由(2)同理得∠DOP=![]() +
+![]()
![]() - 90° ,∠FOQ=
- 90° ,∠FOQ=![]() +
+![]()
![]() -90°
-90°
∠EOH+∠DOP+∠FOQ=![]() +
+![]()
![]() -90°+
-90°+![]() +
+![]()
![]() - 90°+
- 90°+![]() +
+![]()
![]() -90°=
-90°=![]()
解得![]() α+
α+![]() (β+γ)=270°
(β+γ)=270°
∵β+γ=180°-α(三角形内角和180°)
![]()
解得α=90°
∴ △ABC是直角三角形


科目:初中数学 来源: 题型:
【题目】如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.
(1)求证:四边形ABCD是菱形;
(2)若纸条宽3cm,∠ABC=60°,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ADC=130°,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,交对边于F、E,且∠ABF=∠AED,过E作EH⊥AD交AD于H。
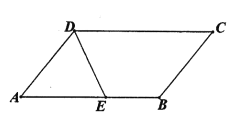
(1)在图中作出线段BF和EH(不要求尺规作图);
(2)求∠AEH的大小。
小亮同学根据条件进行推理计算,得出结论,请你在括号内注明理由。
证明:∵BF、DE分别平分∠ABC与∠ADC,(已知)
∴∠ABF=![]() ∠ABC,∠CDE=
∠ABC,∠CDE=![]() ∠ADC。( )
∠ADC。( )
∵∠ABC=∠ADC,(已知)
∴∠ABF=∠CDE。(等式的性质)
∵∠ABF=∠AED,(已知)
∴∠CDE=∠AED。( )
∴AB∥CD。( )
∵∠ADC=130°(已知)
∴∠A=180°-∠ADC=50°(两直线平行,同旁内角互补)
∵EH⊥AD于H(已知)
∴∠EHA=90°(垂直的定义)
∴在Rt△AEH中,∠AEH=90°-∠A( )=40°。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要900元;若购进甲种花卉40盆,乙种花卉30盆,需要960元.
(1)求购进甲、乙两种花卉每盆各需多少元?
(2)该花店购进甲,乙两种花卉共100盆,甲种花卉每盆售价20元,乙种花齐每盆售价16元,现该花店把100盆花卉全部售出,若获利超过480元,则至少购进甲种花卉多少盆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,DE平分∠ADC交BC于点E,将一块三角板的直角顶点放在E点处,并使它的一条直角边过点A,另一条直角边交CD于M点.若点M为CD中点,BC=6,则BE的长为( )
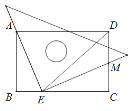
A. 2B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
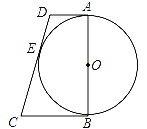
【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铜陵某初中根据教育部在中小学生中每天开展体育活动一小时的通知要求,共开设了排球、篮球、体操、羽毛球四项体育活动课,全校每个学生都可根据自己的爱好任选其中一项.体育老师在所有学生报名中,随机抽取了部分学生的报名情况进行了统计,并将结果整理后绘制了如图两幅不完整的统计图

根据以上统计图解答:
(1)体育老师随机抽取了______名学生,并将条形图补充完整;
(2)在扇形统计图中,求“排球”部分所对应的圆心角的度数并补全扇形统计图;
(3)若学校一共有1600名学生,请估计该校报名参加“篮球”这一项目的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com