
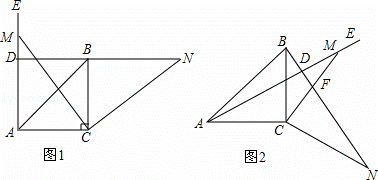
如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.
(1)直接写出∠NDE的度数;
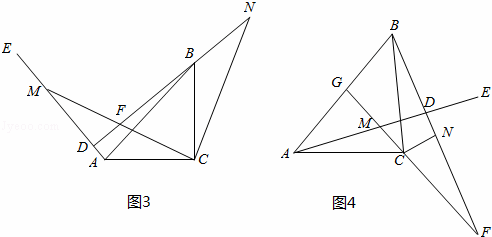
(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;
(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=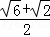 ,其他条件不变,求线段AM的长.
,其他条件不变,求线段AM的长.
| 本题考查的是矩形的判定和性质以及三角形全等的判定和性质,正确作出辅助线、利用方程的思想是解题的关键,注意旋转的性质的灵活运用. |


科目:初中数学 来源: 题型:
理解:数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:
思路一 如图1, 在Rt△ABC中,∠C=90°,∠ABC=30°,延
在Rt△ABC中,∠C=90°,∠ABC=30°,延
 长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=
长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC= .tanD=tan15°=
.tanD=tan15°= =
= =2﹣
=2﹣ .
.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)= .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)= =
= =2﹣
=2﹣ .
.
思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
(3)拓展:如图3,直线y= x﹣1与双曲线y=
x﹣1与双曲线y= 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
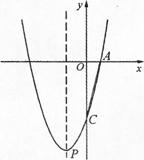
已知二次函数 的图象与y轴的交点为C,与x轴正半轴的交点为A.且
的图象与y轴的交点为C,与x轴正半轴的交点为A.且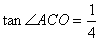 .
.
(1)求二次函数的解析式;
(2)P为二次函数图象的顶点, Q为其对称轴上的一点,QC平分∠PQO,求Q点坐标;
Q为其对称轴上的一点,QC平分∠PQO,求Q点坐标;
(3)是否存在实数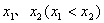 ,当
,当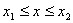 时,y的取值范围为
时,y的取值范围为 .若存在,直接写出x1,x2的值;若不存在,说明理由.
.若存在,直接写出x1,x2的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com