
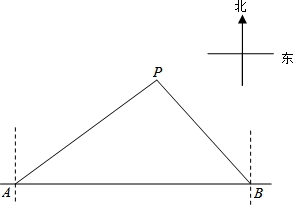
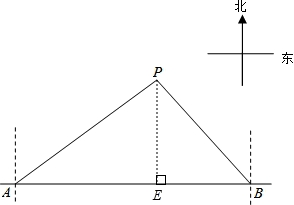
马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50°方向上,在救助船B的西北方向上,船B在船A正东方向140海里处.(参考数据:sin36.5°≈0.6,cos36.5°≈0.8,tan36.5°≈0.75).
(1)求可疑漂浮物P到A、B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.
【考点】解直角三角形的应用-方向角问题.
【专题】几何图形问题.
【分析】(1)过点P作PE⊥AB于点E,在Rt△APE中解出PE即可;
(2)分别求出PA、PB的长,根据两船航行速度,计算出两艘船到达P点时各自所需要的时间,即可作出判断.
【解答】解:(1)过点P作PE⊥AB于点E,
由题意得,∠PAE=36.5°,∠PBA=45°,
设PE为x海里,则BE=PE=x海里,
∵AB=140海里,
∴AE=(140﹣x)海里,
在Rt△PAE中,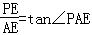 ,
,
即: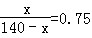
解得:x=60,
∴可疑漂浮物P到A、B两船所在直线的距离约为60海里;
(2)在Rt△PBE中,PE=60海里,∠PBE=45°,
则BP=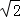 PE=60
PE=60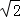 ≈84.8海里,
≈84.8海里,
B船需要的时间为:84.8÷30≈2.83小时,
在Rt△PAE中,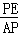 =sin∠PAE,
=sin∠PAE,
∴ AP=PE÷sin∠PAE=60÷0.6=100海里,
AP=PE÷sin∠PAE=60÷0.6=100海里,
∴A船需要的时间为:100÷40=2.5小时,
∵2.83>2.5,
∴A船先到达.
【点评】本题考查了解直角三角形的应用,解答本题的关键是理解方位角的定义,能利用三角函数值计算有关线段,难度一般.


科目:初中数学 来源: 题型:
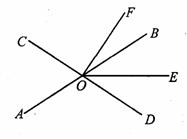
如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
 (2)若OF平分∠COE,∠BOF=15°,求∠AOC的度数.
(2)若OF平分∠COE,∠BOF=15°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
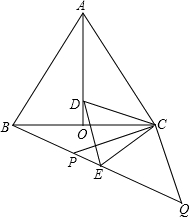
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE;
(2)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com