
【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利过程.下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题: 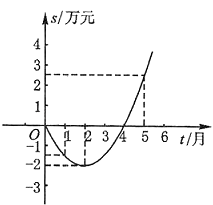
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润是多少万元?
【答案】
(1)解:由图象可知其顶点坐标为(2,﹣2),
故可设其函数关系式为:S=a(t﹣2)2﹣2.
∵所求函数关系式的图象过(0,0),
于是得:
a(0﹣2)2﹣2=0,
解得a= ![]() .
.
∴所求函数关系式为:S= ![]() (t﹣2)2﹣2,即S=
(t﹣2)2﹣2,即S= ![]() t2﹣2t.
t2﹣2t.
答:累积利润S与时间t之间的函数关系式为:S= ![]() t2﹣2t
t2﹣2t
(2)解:把S=30代入S= ![]() (t﹣2)2﹣2,
(t﹣2)2﹣2,
得 ![]() (t﹣2)2﹣2=30.
(t﹣2)2﹣2=30.
解得t1=10,t2=﹣6(舍去).
答:截止到10月末公司累积利润可达30万元
(3)解:把t=7代入关系式,
得S= ![]() ×72﹣2×7=10.5,
×72﹣2×7=10.5,
把t=8代入关系式,
得S= ![]() ×82﹣2×8=16,
×82﹣2×8=16,
16﹣10.5=5.5,
答:第8个月公司所获利是5.5万元
【解析】(1)本题是通过构建函数模型解答销售利润的问题,应根据图象以及题目中所给的信息来列出S与t之间的函数关系式;(2)把S=30代入累计利润S= ![]() t2﹣2t的函数关系式里,求得月份;(3)分别t=7,t=8,代入函数解析S=
t2﹣2t的函数关系式里,求得月份;(3)分别t=7,t=8,代入函数解析S= ![]() t2﹣2t,再把总利润相减就可得出.
t2﹣2t,再把总利润相减就可得出.


科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.
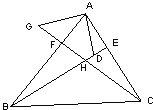
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,∠ABC+∠ADC=180°,AB=BC.
(1)如图1,若∠BAD=90°,AD=2,求CD的长度;
(2)如图2,点P、Q分别在线段AD、DC上,满足PQ=AP+CQ,求证:∠PBQ=90°![]() ∠ADC;
∠ADC;
(3)如图3,若点Q运动到DC的延长线上,点P也运动到DA的延长线上时,仍然满足PQ=AP+CQ,则(2)中的结论是否成立?若成立,请给出证明过程,若不成立,请写出∠PBQ与∠ADC的数量关系,并给出证明过程.
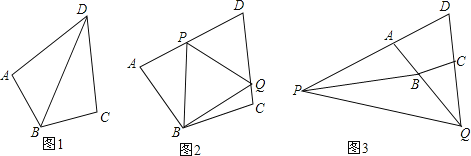
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0). 
(1)请直接写出于点B关于坐标原点O的对称点B1的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出对应的△A′B′C′图形,直接写出点A的对应点A′的坐标;
(3)若四边形A′B′C′D′为平行四边形,请直接写出第四个顶点D′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P(﹣3,m)和Q(1,m)是抛物线y=2x2+bx+1上的两点.
(1)求b的值;
(2)将抛物线y=2x2+bx+1的图象向上平移k(k是正整数),使平移后的图象的顶点在x轴上,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( ) 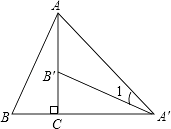
A.70°
B.65°
C.60°
D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y= ![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣ ![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( ) 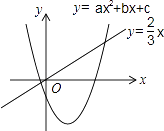
A.大于0
B.等于0
C.小于0
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东昌湖举行的健身运动会龙舟比赛中,甲、乙两队在500米的赛道上,所滑行的路程y(m)与实践x(min)之间的函数关系如图所示,下列说法正确的有____________.
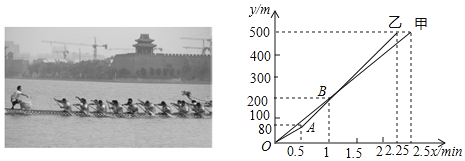
①乙队比甲队提前0. 25min到达终点.
②当乙队划行110m时,此时落后甲队15m.
③0. 5min后,乙队比甲队每分钟快40m.
④自1. 5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到255m/min.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com