【题目】在东昌湖举行的健身运动会龙舟比赛中，甲、乙两队在500米的赛道上，所滑行的路程y(m)与实践x(min)之间的函数关系如图所示，下列说法正确的有____________.
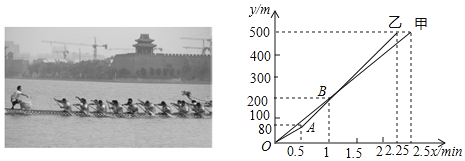
①乙队比甲队提前0. 25min到达终点.
②当乙队划行110m时，此时落后甲队15m.
③0. 5min后，乙队比甲队每分钟快40m.
④自1. 5min开始，甲队若要与乙队同时到达终点，甲队的速度需要提高到255m/min.
【答案】①②③
【解析】
解：A．由横坐标看出乙队比甲队提前0.25min到达终点，故A不符合题意；
B．乙AB段的解析式为y=240x﹣40，当y=110时，x=
；甲的解析式为y=200x，当x=时，y=125，当乙队划行110m时，此时落后甲队15m，故B不符合题意；
C．乙AB段的解析式为y=240x﹣40，乙的速度是240m/min；甲的解析式为y=200x，甲的速度是200m/min，0.5min后，乙队比甲队每分钟快40m，故C不符合题意；
D．甲的解析式为y=200x，当x=1.5时，y=300，甲乙同时到达（500﹣300）÷（2.25﹣1.5）≈267m/min，故D符合题意；
故选D．
科目：初中数学 来源： 题型：
【题目】某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利过程．下面的二次函数图象（部分）刻画了该公司年初以来累积利润s（万元）与销售时间t（月）之间的关系（即前t个月的利润总和s和t之间的关系）．根据图象提供的信息，解答下列问题：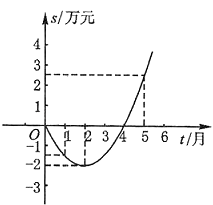 
（1）由已知图象上的三点坐标，求累积利润s（万元）与时间t（月）之间的函数关系式；
（2）求截止到几月末公司累积利润可达到30万元；
（3）求第8个月公司所获利润是多少万元？
查看答案和解析>>
科目：初中数学 来源： 题型：
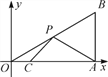
【题目】如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为(3， 
)，点C的坐标为(
，0)，点P为斜边OB上的一个动点，则PA＋PC的最小值为( )
A. 
B. 
C. 
D. 2 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了拉动内需，让惠于农民，丰富农民的业余生活，鼓励送彩电下乡，国家决定实行政府补贴．规定每购买一台彩电，政府补贴若干元，经调查某商场销售彩电台数y（台）与补贴款额x（元）之间大致满足如图所示的一次函数关系．随着补贴款额x的不断增大，销售量也不断增加，但每台彩电的收益p（元）会相应降低且满足：p=﹣ 
x+110（x≥0）．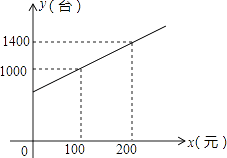 
（1）在政府补贴政策实施后，求出该商场销售彩电台数y与政府补贴款额x之间的函数关系式；
（2）在政府未出台补贴措施之前，该商场销售彩电的总收益额为多少元？
（3）要使该商场销售彩电的总收益最大，政府应将每台补贴款额x定为多少？并求出总收益的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，对于任意三点
的“矩面积”，给出如下定义:“水平底”
为任意两点横坐标差的最大值，“铅垂高”
为任意两点纵坐标差的最大值，则“矩面积”
.
例如:三点坐标分别为
，则“水平底”
，“铅垂高”
，“矩面积”
.
(1)已知点
.
①若
三点的“矩面积”为12，求点
的坐标;
②求三点的“矩面积”的最小值.
(2)已知点
，其中
.若
三点的“矩面积”为8，求
的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满．当每个房间每天的房价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的房价不得高于340元．设每个房间的房价增加x元（x为10的正整数倍）．
（1）设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；
（2）设宾馆一天的利润为w元，求w与x的函数关系式；
（3）一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为⊙O的直径，弦CD⊥AB于E，∠CDB=15°，OE=2 
． 
（1）求⊙O的半径；
（2）将△OBD绕O点旋转，使弦BD的一个端点与弦AC的一个端点重合，则弦BD与弦AC的夹角为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
