
【题目】如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2 ![]() .
. 
(1)求⊙O的半径;
(2)将△OBD绕O点旋转,使弦BD的一个端点与弦AC的一个端点重合,则弦BD与弦AC的夹角为 .
【答案】
(1)解:∵AB为⊙O的直径,弦CD⊥AB于E,
∴弧BC=弧BD,
∴∠BDC= ![]() ∠BOD,
∠BOD,
而∠CDB=15°,
∴∠BOD=2×15°=30°,
在Rt△ODE中,∠DOE=30°,OE=2 ![]() ,
,
∴OE= ![]() DE,OD=2DE,
DE,OD=2DE,
∴DE= ![]() =2,
=2,
∴OD=4,
即⊙O的半径为4
(2)60°或90°
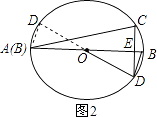
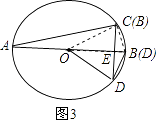
【解析】解: (2)有4种情况:如图: 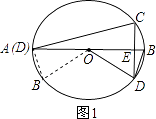

①如图1所示:∵OA=OB,∠AOB=30°,
∴∠OAB=∠OBA=75°,
∵CD⊥AB,AB是直径,
∴弧BC=弧BD,
∴∠CAB= ![]() ∠BOD=15°,
∠BOD=15°,
∴∠CAB=∠BAO+∠CAB=15°+75°=90°;
②如图2所示,∠CAD=75°﹣15°=60°;
③如图3所示:∠ACB=90°;
④如图4所示:∠ACB=60°;
所以答案是:60°或90°.
【考点精析】通过灵活运用勾股定理的概念和垂径定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y= ![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣ ![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( ) 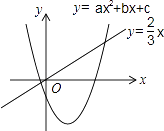
A.大于0
B.等于0
C.小于0
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东昌湖举行的健身运动会龙舟比赛中,甲、乙两队在500米的赛道上,所滑行的路程y(m)与实践x(min)之间的函数关系如图所示,下列说法正确的有____________.
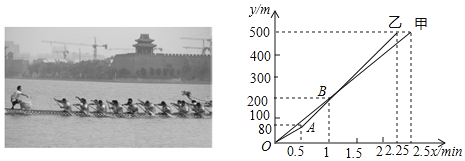
①乙队比甲队提前0. 25min到达终点.
②当乙队划行110m时,此时落后甲队15m.
③0. 5min后,乙队比甲队每分钟快40m.
④自1. 5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到255m/min.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解射击运动员小杰的集训效果,教练统计了他集训前后的两次测试成绩(每次测试射击10次),制作了如图所示的条形统计图.
(1)集训前小杰射击成绩的众数为 ;
(2)分别计算小杰集训前后射击的平均成绩;
(3)请用一句话评价小杰这次集训的效果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用长为28米长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设AB=x米,花园面积S. 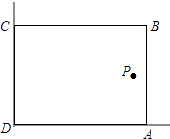
(1)写出S 关于x的函数解析式,当S=192平方米,求x的值;
(2)若在P处有一棵树与墙CD、AD的距离分别是15米和6米,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,

(1)求高台A比矮台B高多少米?
(2)求旗杆的高度OM;
(3)玛丽在荡绳索过程中离地面的最低点的高度MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
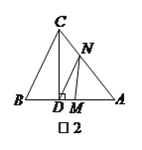
【题目】如图![]() ,
, ![]() 中,
中, ![]() 于
于![]() ,且
,且![]() .
.
(![]() )试说明
)试说明![]() 是等腰三角形.
是等腰三角形.
(![]() )已知
)已知![]() ,如图
,如图![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 的速度沿线段
的速度沿线段![]() 向点
向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发以相同速度沿线段
出发以相同速度沿线段![]() 向点
向点![]() 运动,当其中一点到达终点时整个运动都停止.设点
运动,当其中一点到达终点时整个运动都停止.设点![]() 运动的时间为
运动的时间为![]() (秒).
(秒).
①若![]() 的边与
的边与![]() 平行,求
平行,求![]() 的值.
的值.
②若点![]() 是边
是边![]() 的中点,问在点
的中点,问在点![]() 运动的过程中,
运动的过程中, ![]() 能否成为等腰三角形?若能,求出
能否成为等腰三角形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com