练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若二次函数y=（k﹣2）x2+2x+1的图象与x轴有交点，则k的取值范围是 ．

    【答案】k≤3且k≠2
    【解析】解：∵二次函数y=（k﹣2）x2+2x+1的图象与x轴有交点， ∴一元二次方程（k﹣2）x2+2x+1=0有解，
    ∴ ，
    解得：k≤3且k≠2．
    所以答案是：k≤3且k≠2．
    【考点精析】根据题目的已知条件，利用抛物线与坐标轴的交点的相关知识可以得到问题的答案，需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（ ， ）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．

    （1）求抛物线的解析式；
    （2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，对于任意三点的“矩面积”，给出如下定义:“水平底”为任意两点横坐标差的最大值，“铅垂高”为任意两点纵坐标差的最大值，则“矩面积”.

    例如:三点坐标分别为，则“水平底”，“铅垂高”，“矩面积”.

    (1)已知点.

    ①若三点的“矩面积”为12，求点的坐标;

    ②求三点的“矩面积”的最小值.

    (2)已知点，其中.若三点的“矩面积”为8，求的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满．当每个房间每天的房价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的房价不得高于340元．设每个房间的房价增加x元（x为10的正整数倍）．
    （1）设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；
    （2）设宾馆一天的利润为w元，求w与x的函数关系式；
    （3）一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：

    （Ⅰ）图1中a的值为 ；

    （Ⅱ）求统计的这组初赛成绩数据的平均数、众数和中位数；

    （Ⅲ）根据这组初赛成绩，由高到低确定9人进入复赛，请直接写出初赛成绩为1.65m的运动员能否进入复赛．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，弦CD⊥AB于E，∠CDB=15°，OE=2 ．
    （1）求⊙O的半径；
    （2）将△OBD绕O点旋转，使弦BD的一个端点与弦AC的一个端点重合，则弦BD与弦AC的夹角为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果多边形的每个内角都比它相邻的外角的4倍多30°，求这个多边形的内角和及对角线的总条数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（　　）

    A. 1 B. C. D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y=ax2+bx+c的图象开口向上，对称轴为直线x=1，图象经过（3，0），下列结论中，正确的一项是（ ）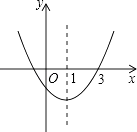
    A.abc＜0
    B.4ac﹣b2＜0
    C.a﹣b+c＜0
    D.2a+b＜0

    查看答案和解析>>

    同步练习册答案