
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0). 
(1)请直接写出于点B关于坐标原点O的对称点B1的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出对应的△A′B′C′图形,直接写出点A的对应点A′的坐标;
(3)若四边形A′B′C′D′为平行四边形,请直接写出第四个顶点D′的坐标.
【答案】
(1)解:B1(6,0)
(2)解:如图所示:A′(﹣3,﹣2)
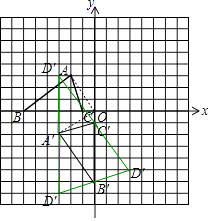
(3)解:如图所示:D′(3,﹣5)或(﹣3,3)或(﹣3,﹣7).

【解析】(1)根据关于原点对称的点的坐标特点:两个点关于原点对称时,它们的坐标符号相反可直接写出答案;(2)首先确定A、B、C三点绕坐标原点O逆时针旋转90°后的对应点位置,然后再连接即可;(3)分别以A′C′,B′A′,C′B′为对角线画出平行四边形,可得D′的坐标.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系. 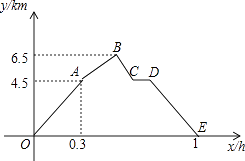
(1)小明骑车在平路上的速度为km/h;他途中休息了h;
(2)求线段AB、BC所表示的y与x之间的函数关系式;
(3)如果小明两次经过途中某一地点的时间间隔为0.15h,那么该地点离甲地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
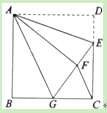
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小商场以每件20元的价格购进一种服装,先试销一周,试销期间每天的销量(件)与每件的销售价x(元/件)如下表:
x(元/件) | 38 | 36 | 34 | 32 | 30 | 28 | 26 |
t(件) | 4 | 8 | 12 | 16 | 20 | 24 | 28 |
假定试销中每天的销售量t(件)与销售价x(元/件)之间满足一次函数.
(1)试求t与x之间的函数关系式;
(2)在商品不积压且不考虑其它因素的条件下,每件服装的销售定价为多少时,该小商场销售这种服装每天获得的毛利润最大?每天的最大毛利润是多少?(注:每件服装销售的毛利润=每件服装的销售价﹣每件服装的进货价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=ax2+bx+c如图所示,下列四个结论: ①abc<0;②b﹣2a<0;③a﹣b+c<0;④b2﹣4ac>0.
其中正确结论的个数是( )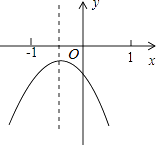
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
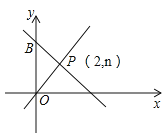
【题目】如图,一次函数y=-x+m的图象与x轴和y轴分别交于点A和点B,与正比例函数![]() 图象交于点P(2,n).
图象交于点P(2,n).
(1)求m和n的值;
(2)求△POB的面积;
(3)在直线OP上是否存在异与点P的另一点C,使得△OBC与△OBP的面积相等?若存在,请求出C点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利过程.下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题: 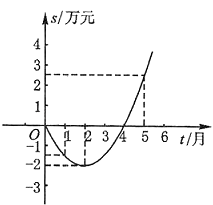
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 、
、![]() 的垂直平分线相交于三角形内一点
的垂直平分线相交于三角形内一点![]() ,下列结论中,错误的是( )
,下列结论中,错误的是( )
A. 点![]() 在
在![]() 的垂直平分线上
的垂直平分线上
B. ![]() 、
、![]() 、
、![]() 都是等腰三角形
都是等腰三角形
C. ![]()
D. 点![]() 到
到![]() 、
、![]() 、
、![]() 的距离相等
的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益p(元)会相应降低且满足:p=﹣ ![]() x+110(x≥0).
x+110(x≥0). 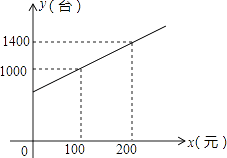
(1)在政府补贴政策实施后,求出该商场销售彩电台数y与政府补贴款额x之间的函数关系式;
(2)在政府未出台补贴措施之前,该商场销售彩电的总收益额为多少元?
(3)要使该商场销售彩电的总收益最大,政府应将每台补贴款额x定为多少?并求出总收益的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com