
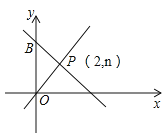
【题目】如图,一次函数y=-x+m的图象与x轴和y轴分别交于点A和点B,与正比例函数![]() 图象交于点P(2,n).
图象交于点P(2,n).
(1)求m和n的值;
(2)求△POB的面积;
(3)在直线OP上是否存在异与点P的另一点C,使得△OBC与△OBP的面积相等?若存在,请求出C点的坐标;若不存在,请说明理由.
【答案】(1)m的值为5,n的值为3.(2)5;(3)点C的坐标为(﹣2,﹣3).
【解析】试题(1)先把P(2,n)代入y=![]() x即可得到n的值,从而得到P点坐标为(2,3),然后把P点坐标代入y=-x+m可计算出m的值;
x即可得到n的值,从而得到P点坐标为(2,3),然后把P点坐标代入y=-x+m可计算出m的值;
(2)先利用一次函数解析式确定B点坐标,然后根据三角形面积公式求解即可;
(3)根据△OBC与△OBP有一条公共边,可知点C横坐标的绝对值与点P横坐标的绝对值相等,根据题意即可确定出点C的横坐标,代入解析式即可得到点C的坐标.
试题解析:(1)∵点P(2,n)在正比例函数y=![]() x图象上,
x图象上,
∴n=![]() ×2=3,
×2=3,
∴点P的坐标为(2,3),
∵点P(2,3)在一次函数y=﹣x+m的图象上,
∴3=﹣2+m,解得:m=5,
∴一次函数解析式为y=﹣x+5,
∴m的值为5,n的值为3;
(2)当x=0时,y=﹣x+5=5,
∴点B的坐标为(0,5),
∴S△POB=![]() OBxP=
OBxP=![]() ×5×2=5;
×5×2=5;
(3)存在,
∵S△OBC=![]() OB|xC|=S△POB=5,
OB|xC|=S△POB=5,
∴xC=﹣2或xC=2(舍去),
当x=﹣2时,y=![]() ×(﹣2)=﹣3,
×(﹣2)=﹣3,
∴点C的坐标为(﹣2,﹣3).


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l经过点A(﹣3,0),点B(0, ![]() ),点P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左平移,平移后得到⊙P′(点P的对应点为点P′),当⊙P′与直线l相交时,横坐标为整数的点P′共有( )
),点P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左平移,平移后得到⊙P′(点P的对应点为点P′),当⊙P′与直线l相交时,横坐标为整数的点P′共有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=120°,DE垂直平分AC交BC于D,垂足为E,若DE=2cm,则BC的长为( )
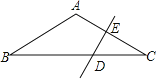
A. 6cm B. 8cm C. 10cm D. 12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0). 
(1)请直接写出于点B关于坐标原点O的对称点B1的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出对应的△A′B′C′图形,直接写出点A的对应点A′的坐标;
(3)若四边形A′B′C′D′为平行四边形,请直接写出第四个顶点D′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
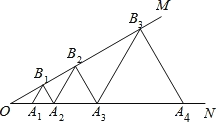
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( ) 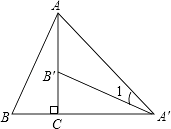
A.70°
B.65°
C.60°
D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com