
【题目】如图,若△ABC和△DEF的面积分别为S1、S2 , 则( ) 
A.S1= ![]() S2
S2
B.S1= ![]() S2
S2
C.S1=S2
D.S1= ![]() S2
S2
【答案】C
【解析】解:过A点作AG⊥BC于G,过D点作DH⊥EF于H. 在Rt△ABG中,AG=ABsin40°=5sin40°,
∠DEH=180°﹣140°=40°,
在Rt△DHE中,DH=DEsin40°=8sin40°,
S1=8×5sin40°÷2=20sin40°,
S2=5×8sin40°÷2=20sin40°.
则S1=S2 .
故选:C.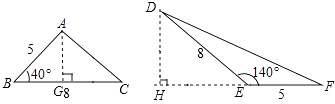
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.
(1)如图,若BC=BD,求证:CD=DE;
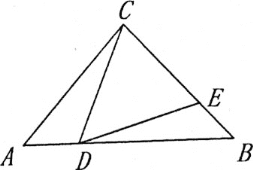
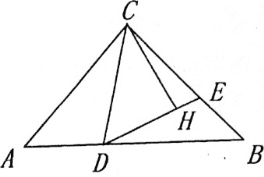
(2)如图,过点C作CH⊥DE,垂足为H,若CD=BD,![]() ,直接写出CE-BE的值为________.
,直接写出CE-BE的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点,与y轴交于点C,顶点为D,抛物线的对称轴DF与BC相交于点E,与x轴相交于点F.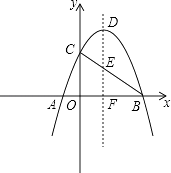
(1)求线段DE的长;
(2)设过E的直线与抛物线相交于点M(x1 , y1),N(x2 , y2),试判断当|x1﹣x2|的值最小时,直线MN与x轴的位置关系,并说明理由;
(3)设P为x轴上的一点,∠DAO+∠DPO=∠α,当tan∠α=4时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系. 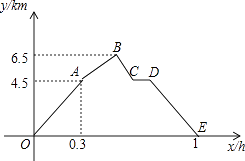
(1)小明骑车在平路上的速度为km/h;他途中休息了h;
(2)求线段AB、BC所表示的y与x之间的函数关系式;
(3)如果小明两次经过途中某一地点的时间间隔为0.15h,那么该地点离甲地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,折线段AOB将面积为S的⊙O分成两个扇形,大扇形、小扇形的面积分别为S1、S2 , 若 ![]() =0.618,则称分成的小扇形为“黄金扇形”.生活中的折扇(如图2)大致是“黄金扇形”,则“黄金扇形”的圆心角约为°.(精确到0.1)
=0.618,则称分成的小扇形为“黄金扇形”.生活中的折扇(如图2)大致是“黄金扇形”,则“黄金扇形”的圆心角约为°.(精确到0.1) 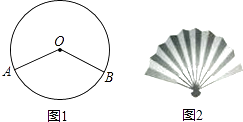
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
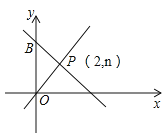
【题目】如图,一次函数y=-x+m的图象与x轴和y轴分别交于点A和点B,与正比例函数![]() 图象交于点P(2,n).
图象交于点P(2,n).
(1)求m和n的值;
(2)求△POB的面积;
(3)在直线OP上是否存在异与点P的另一点C,使得△OBC与△OBP的面积相等?若存在,请求出C点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com