
【题目】如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画![]() ,P是
,P是![]() 上一动点,且P在第一象限内,过点P作
上一动点,且P在第一象限内,过点P作![]() 的切线与x轴相交于点A,与y轴相交于点B.在
的切线与x轴相交于点A,与y轴相交于点B.在![]() 上存在点Q,使得以Q、O、A、P为顶点的四边形是平行四边形,请写出Q点的坐标_________.
上存在点Q,使得以Q、O、A、P为顶点的四边形是平行四边形,请写出Q点的坐标_________.

【答案】![]() 或
或![]()
【解析】
分两种情况:OPAQ为平行四边形时,得出OQ⊥OP,AQ⊥AB,进而得出△POQ是等腰直角三角形,得出∠AOQ=∠AOP=45°,即可得出Q点坐标;OAPQ为平行四边形时,同理也可得出Q点坐标.
分两种情况:
如图OPAQ为平行四边形,
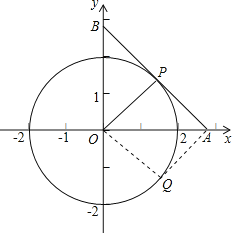
∴PO∥QA,OQ∥PA;
∵AB⊥OP,
∴OQ⊥OP,AQ⊥AB,
∴∠POQ=90°,
∵OP=OQ,
∴△POQ是等腰直角三角形,
∴OA是∠POQ的平分线且是边PQ上的中垂线,
∴∠AOQ=∠AOP=45°,
∴∠BOP=45°,
设P(x,x)、Q(x,-x)(x>0),
∵OP=2
∴![]() 解得
解得![]()
∴Q点坐标是![]()
②如图示OAPQ为平行四边形,
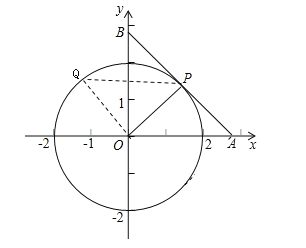
同理可得Q点坐标是![]()


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在点
在点![]() 左侧.点
左侧.点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
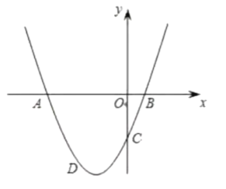
(1)求抛物线的解析式;
(2)当![]() 时,如图所示,若点
时,如图所示,若点![]() 是第三象限抛物线上方的动点,设点
是第三象限抛物线上方的动点,设点![]() 的横坐标为
的横坐标为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() ,求出
,求出![]() 与
与![]() 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量![]() 的取值范围;请问当
的取值范围;请问当![]() 为何值时,
为何值时,![]() 有最大值?最大值是多少.
有最大值?最大值是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和同学们在学习圆的基本性质时发现了一个结论:如图1,圆![]() 中
中![]() ,
,![]() 是圆中的两条弦,
是圆中的两条弦,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() .
.
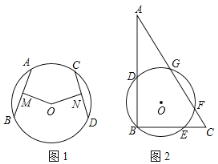
(1)请帮小明证明这个结论;
(2)请参考小明思考问题的方法解决问题,如图2,在![]() 中,
中,![]() ,
,![]() 为
为![]() 的内心,以
的内心,以![]() 为圆心,
为圆心,![]() 为半径的圆与
为半径的圆与![]() 三边分别相交于点
三边分别相交于点![]() 、
、![]() 、
、![]() 、
、![]() . 若
. 若![]() ,
,![]() ,求
,求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小李准备七月初到重庆或长沙去旅游,为了了解这两个城市哪个更热,他们查阅资料,收集了两个城市2018年七月前两周最高温度的记录,如下表:
日期(七月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
重庆最高温度/℃ | 33 | 36 | 34 | 31 | 31 | 30 | 30 | 33 | 34 | 36 | 37 | 35 | 37 | 37 |
长沙最高温度/℃ | 29 | 34 | 35 | 35 | 36 | 29 | 31 | 31 | 34 | 35 | 35 | 31 | 35 | 35 |
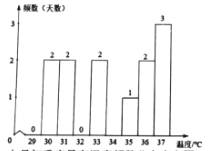
根据上表,他们将两个城市的最高温度分别绘制了如下的频数分布直方图和统计表,并对数据进行了整理
七月初重庆最高温度频数分布直方图
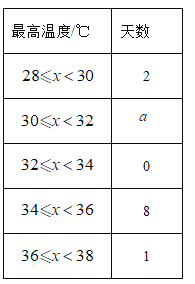
七月初长沙最高温度统计表
平均数/℃ | 中位数/℃ | 众数/℃ | 34/℃以上天数 | 30/℃以下天数 | |
重庆 | 33.9 | 34 | c | 6 | 0 |
长沙 | 33.2 | b | 35 | 7 | 2 |
请回答如下问题:
(1)本次调查的目的是________;
(2)补全频数分布直方图,并写出表中a,b,c的值,![]() ________,
________,![]() _____,c=___.
_____,c=___.
(3)结合以上分析,你认为七月初哪个城市更热,请写出两条支持你观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,F是⊙O上一点,连接FO、FB.C为![]() 中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
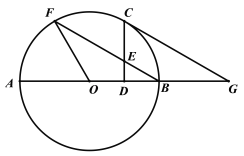
(1)求证:CG是⊙O的切线;
(2)若![]() BOF=120°,且CE=4,求⊙O的半径.
BOF=120°,且CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解决问题.
小聪在探索三角形中位线性质定理证明的过程中,得到了如下启示:一条线段经过另一线段的中点,则延长前者,并且长度相等,就能构造全等三角形.如图,D是△ABC的AC边的中点,E为AB上任一点,延长ED至F,使DF=DE,连接CF,则可得△CFD≌△AED,从而把△ABC剪拼成面积相等的四边形BCFE.你能从小聪的反思中得到启示吗?
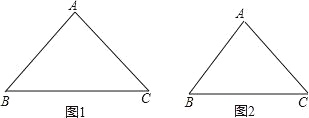
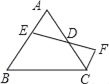
(1)如图1,已知△ABC,试着剪一刀,使得到的两块图形能拼成平行四边形.
①把剪切线和拼成的平行四边形画在图1上,并指出剪切线应符合的条件.
②思考并回答:要使上述剪拼得到的平行四边形成为矩形,△ABC的边或角应符合什么条件?菱形呢?正方形呢?(直接写出用符号表示的条件)
(2)如图2,已知锐角△ABC,试着剪两刀,使得到的三块图形能拼成矩形,把剪切线和拼成的矩形画在图2上,并指出剪切线应符合的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
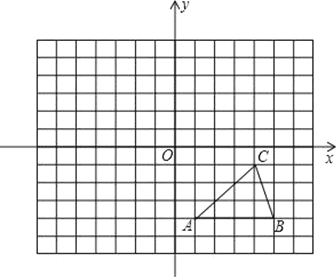
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出A1的坐标;
(2)以原点O为对称中心,再画出与△A1B1C1关于原点O对称的△A2B2C2,并写出点A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com