Question

19．在?ABCD中，∠ABC的角平分线BE交AD所在直线于点E，AD=5，DE=1，则AB=4或6．

Answer 1

分析 分两种情况：①如图1，在?ABCD中，根据平行线和角平分线的性质得到△ABE是等腰三角形，于是得到AB=AE，根据已知条件即可得到结果；
②如图2，方法同①．

解答 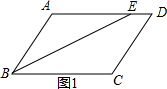解：①如图1，在?ABCD中，
∵AD∥BC，
∴∠AEB=∠CBE，
∵BE平分∠ABC，
∴∠ABE=∠EBC，
∴∠ABE=∠AEB，
∴AB=AE，
∵AD=5，DE=1，
∴AB=AE=4；
②如图2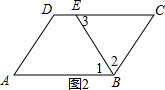，在?ABCD中，
∵AB∥DC，BC=AD=5，AB=CD，
∴∠1=∠3，
∵BE平分∠ABC，
∴∠1=∠2，
∴∠2=∠3，
∴BC=CE，
∵BC=5，
∴CE=5，∵DE=1，
∴AB=CD=6，
综上所述：AB=4或6，
故答案为：4或6．

点评 本题主要考查对平行四边形的性质，平行线的性质，角平分线的性质，等腰三角形的判定等知识点的理解和掌握，能综合运用这些性质进行计算是解此题的关键．