
分析 首先利用平方差公式展开,然后计算后得到$\frac{1}{2}$×$\frac{2016}{2015}$,从而求解结果.
解答 解:原式=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)…(1+$\frac{1}{2015}$)
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$…$\frac{2016}{2015}$
=$\frac{1}{2}$×$\frac{2016}{2015}$
=$\frac{1008}{2015}$.
点评 本题考查了因式分解的应用,解题的关键是能够利用因式分解分解后发现中间所有项的积为1,难度不大.


科目:初中数学 来源: 题型:填空题
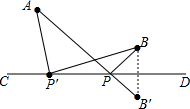 如图所示,直线CD同侧有两个点A,B,在CD上找一点P使得AP+BP最短,并说明理由,盼盼的解题思路如下,请你帮助完成操作及填空
如图所示,直线CD同侧有两个点A,B,在CD上找一点P使得AP+BP最短,并说明理由,盼盼的解题思路如下,请你帮助完成操作及填空查看答案和解析>>
科目:初中数学 来源: 题型:填空题
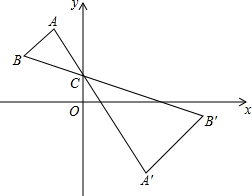 如图,点A、B、C在平面直角坐标系xOy中,点A的坐标为(a,b),点C的坐标为(0,1),△A′B′C是△ABC关于点C的位似图形.若△ABC与△A′B′C的相似比为1:2,则点A′的坐标为(-2a,3-2b).
如图,点A、B、C在平面直角坐标系xOy中,点A的坐标为(a,b),点C的坐标为(0,1),△A′B′C是△ABC关于点C的位似图形.若△ABC与△A′B′C的相似比为1:2,则点A′的坐标为(-2a,3-2b).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1,5 | B. | -$\frac{1}{5}$,5 | C. | -$\frac{2}{3}$,3 | D. | -$\frac{4}{5}$,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
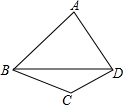 如图,四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=130°,则∠A的度数是( )
如图,四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=130°,则∠A的度数是( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com