
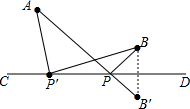
 如图所示,直线CD同侧有两个点A,B,在CD上找一点P使得AP+BP最短,并说明理由,盼盼的解题思路如下,请你帮助完成操作及填空
如图所示,直线CD同侧有两个点A,B,在CD上找一点P使得AP+BP最短,并说明理由,盼盼的解题思路如下,请你帮助完成操作及填空分析 (1)作点B关于CD的对称点B′,连结AB′交CD于点P,连结BP,点P就是所求作的点;
(2)再在CD上另取一点P′,连结AP′,B′P′,根据三角形的三边关系和等量代换即可得到结论.
解答 解:(1)作点B关于CD的对称点B′,连结AB′交CD于点P,连结BP,点P就是所求作的点;
(2)再在CD上另取一点P′,连结AP′,B′P′,
∵AP+BP=AP+PB′(用图中的线段表示)
∵AP′+B′P′>AB′,理由是(三角形的三边关系),
∴AP′+B′P′>AP+BP
∴AP+BP最短.
故答案为:AP+PB′,AB′,三角形的三边关系.
点评 本题考查了利用轴对称变换作图,根据轴对称确定最短路线问题,找出对应点的位置是解题的关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com