
复习课中,教师给出关于x的函数 (k是实数).
(k是实数).
教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.
学生思考后,黑板上出现了一些结论.教师作为活动一员,又补充一些结论,并从中选择如下四条:
①存在函数,其图像经过(1,0)点;
②函数图像与坐标轴总有三个不同的交点;
③当 时,不是y随x的增大而增大就是y随x的增大而减小;
时,不是y随x的增大而增大就是y随x的增大而减小;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数;
教师:请你分别判断四条结论的真假,并给出理由,最后简单写出解决问题时所用的数学方法.
①真,②假,③假,④真,理由和所用的数学方法见解析.
【解析】
试题分析:根据方程思想,特殊与一般思想,反证思想,分类思想对各结论进行判断.
试题解析:①真,②假,③假,④真.理由如下:
①将(1,0)代入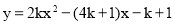 ,得
,得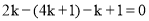 ,解得
,解得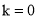 .
.
∴存在函数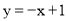 ,其图像经过(1,0)点.
,其图像经过(1,0)点.
∴结论①为真.
②举反例如,当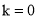 时,函数
时,函数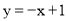 的图象与坐标轴只有两个不同的交点.∴结论②为假.
的图象与坐标轴只有两个不同的交点.∴结论②为假.
③∵当 时,二次函数
时,二次函数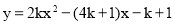 (k是实数)的对称轴为
(k是实数)的对称轴为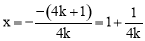 ,
,
∴可举反例如,当 时,二次函数为
时,二次函数为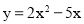 ,
,
当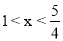 时,y随x的增大而减小;当
时,y随x的增大而减小;当 时,y随x的增大而增大.
时,y随x的增大而增大.
∴结论③为假.
④∵当 时,二次函数
时,二次函数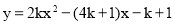 的最值为
的最值为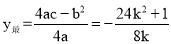 ,
,
∴当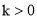 时,有最小值,最小值为负;当
时,有最小值,最小值为负;当 时,有最大值,最大值为正.
时,有最大值,最大值为正.
∴结论④为真.
解决问题时所用的数学方法有方程思想,特殊与一般思想,反证思想,分类思想
考点:1.曲线上点的坐标与方程的关系;2.二次函数的性质;3.方程思想、特殊元素法、反证思想和分类思想的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014年初中毕业升学考试(浙江舟山卷)数学(解析版) 题型:解答题
实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间 (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数 (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当 =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江杭州卷)数学(解析版) 题型:解答题
在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P,求证:PB=PC,并请直接写出图中其他相等的线段.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江宁波卷)数学(解析版) 题型:解答题
作为宁波市政府民生实事之一的公共自行车建设工程已基本完成,某部门对今年4月份中的7天进行了公共自行车日租车辆的统计,结果如下:

(1)求这7天租车辆的众数、中位数和平均数;
(2)用(1)中的平均数估计4月份(30天)共租车多少万车次?
(3)市政府在公共自行车建设项目中共投入9600万元,估计2014年共租车3200万车次,每车次平均收入租车费0.1元,求2014年租车费收入占总投入的百分率(精确到0.1%)
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江西南昌卷)数学(解析版) 题型:选择题
下列运算正确的是( )
A.a2+a3=a5 B.(﹣2a2)3=﹣6a6 C.(2a+1)(2a﹣1)=2a2﹣1 D.(2a3﹣a2)÷a2=2a﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com