
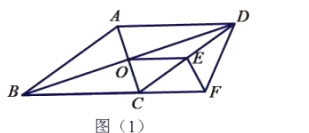
【题目】在菱形![]() 中,点
中,点![]() 是对角线的交点,点
是对角线的交点,点![]() 是边
是边![]() 的中点,点
的中点,点![]() 在
在![]() 延长线上,且
延长线上,且![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 如果
如果![]() ,请写出图中所有的等边三角形.
,请写出图中所有的等边三角形.
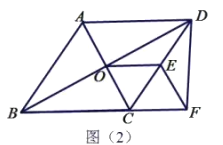
【答案】(1)见解析;(2)![]()
【解析】
(1)根据菱形的性质和三角形中位线的性质可得![]() ,再根据平行四边形的判定和性质可得EF=OC;
,再根据平行四边形的判定和性质可得EF=OC;
(2)由(1)的结论和题意可得![]() 是等边三角形,再由菱形的性质可得OC=
是等边三角形,再由菱形的性质可得OC=![]() AC,从而可得
AC,从而可得![]() 也是等边三角形.
也是等边三角形.
![]() 证明:四边形
证明:四边形![]() 是菱形,
是菱形,![]() ,
,
又∵点E是CD的中点,
![]() ,
,![]()
![]() ,
,
![]() 又,
又,![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ;
;
(2)∵EF=CF,CF=CE,
∴△CEF是等边三角形;
∵四边形![]() 是平行四边形,
是平行四边形,
∴OE=CF,OC=EF,
又∵CE=CF,EF=CF,
∴CE=OE=OC,
△OCE是等边三角形;
∵四边形ABCD是菱形,
∴OC=![]() AC,AD=CD=AB=BC,
AC,AD=CD=AB=BC,
又∵CE=![]() CD,OC=CE,
CD,OC=CE,
∴AC=CD= AD=AB=BC,
∴△ABC,△ACD是等边三角形;
综上所述:图中的等边三角形有:![]() .
.


科目:初中数学 来源: 题型:
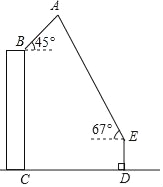
【题目】如图,广场上有一风筝A,小江抓着风筝线的一端站在D处,他从牵引端E测得风筝A的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC=30米)的居民楼顶B处测得风筝A的仰角是45°,已知小江与居民楼的距离CD=40米,牵引端距地面高度DE=1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.414).
≈1.414).
查看答案和解析>>
科目:初中数学 来源: 题型:
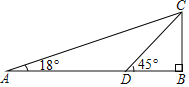
【题目】如图,在某校图书馆门前一段笔直的内部道路AB上,过往车辆限速3米/秒在点B的正上方距其7米高的C处有一个探测仪.一辆轿车从点A匀速向点B行驶5秒后此轿车到达D点,探测仪测得∠CAB=18°,∠CDB=45°,求AD之间的距离,并判断此轿车是否超速,(结果精确到0.01米)(参考数据:sinl8°=0.309,cosl8°=0.951,tanl8°=0.325)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图 1,在△ABC 中,∠ACB=90°,BC=AC,点 D 在 AB 上,DE⊥AB交 BC 于 E,点 F 是 AE 的中点
(1) 写出线段 FD 与线段 FC 的关系并证明;
(2) 如图 2,将△BDE 绕点 B 逆时针旋转α(0°<α<90°),其它条件不变,线段 FD 与线段 FC 的关系是否变化,写出你的结论并证明;
(3) 将△BDE 绕点 B 逆时针旋转一周,如果 BC=4,BE=2![]() ,直接写出线段 BF 的范围.
,直接写出线段 BF 的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠ABC=60°,E为AB中点,F为BC上一点,GカCD上一点,连接EF,FG,且∠BFE=∠CFG.
(1)若G为CD中点吋,求证:EF=FG;
(2)设![]() ,
,![]() ,求y芙于x的函数解析式.
,求y芙于x的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
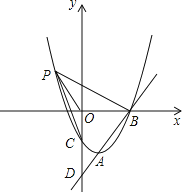
(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,数轴上三个点A、O、P,点O是原点,固定不动,点A和B可以移动,点A表示的数为![]() ,点B表示的数为
,点B表示的数为![]() .
.
(1)若A、B移动到如图所示位置,计算![]() 的值.
的值.
(2)在(1)的情况下,B点不动,点A向左移动3个单位长,写出A点对应的数![]() ,并计算
,并计算![]() .
.
(3)在(1)的情况下,点A不动,点B向右移动15.3个单位长,此时![]() 比
比![]() 大多少?请列式计算.
大多少?请列式计算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与点A重合,点D落到D’处,折痕为EF.
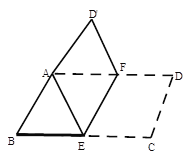
(1)、求证:△ABE≌△AD’F;
(2)、连接CF,判断四边形AECF是否为平行四边形?请证明你的结论。
(3)、若AE=5,求四边形AECF的周长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com