
【题目】【探索新知】
如图1,点C将线段AB分成AC和BC两部分,若BC= ![]() AC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.
AC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.
(1)若AC=3,则AB=_____;
(2)若点D也是图1中线段AB的圆周率点(不同于C点),则AC_____DB;(填“=”或“≠”)
【深入研究】
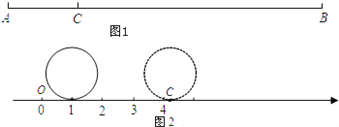
如图2,现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点C的位置.
(3)若点M、N均为线段OC的圆周率点,求线段MN的长度.
【答案】(1)![]() ;(2)=;(3)
;(2)=;(3)![]()
【解析】试题分析:
(1)由题意可知,当AC=3时,可由BC= ![]() AC先求得BC,再由AB=AC+BC可求得AB;
AC先求得BC,再由AB=AC+BC可求得AB;
(2)由题意易得:AB=AC+BC=AC+ ![]() AC=
AC=![]() AC;AB=AD+BD=
AC;AB=AD+BD= ![]() BD+BD=
BD+BD=![]() BD;由此可得AC=BD;
BD;由此可得AC=BD;
(3)由题意可知,OC= ![]() ,设点M是线段OC靠近点O的圆周率点,点N是线段OC靠近点C的圆周率点,则由题意可得:OM
,设点M是线段OC靠近点O的圆周率点,点N是线段OC靠近点C的圆周率点,则由题意可得:OM![]() =
= ![]() ,CN
,CN![]() =
= ![]() ,由此解得:OM=1,CN=1,所以可得MN=OC-OM-CN=
,由此解得:OM=1,CN=1,所以可得MN=OC-OM-CN= ![]() .
.

试题解析:
(1)由题意可知,当AC=3时,BC=![]() ,
,
∴AB=AC+BC=![]() ;
;
(2)由题意可知,AB=AC+BC=AC+ ![]() AC=
AC=![]() AC;
AC;
∵点D是AB上不同于点C的另一个圆周率点,
∴AB=AD+BD= ![]() BD+BD=
BD+BD=![]() BD;
BD;
∴![]() AC=
AC=![]() BD,
BD,
∴AC=BD;
(3)如图2,由题意可知:OC= ![]() .
.
设点M是线段OC靠近点O的圆周率点,点N是线段OC靠近点C的圆周率点,则由题意可得:
OM![]() =
= ![]() ,CN
,CN![]() =
= ![]() ,
,
由此解得:OM=1,CN=1,
∴MN=OC-OM-CN= ![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若点M在抛物线y=(x﹣3)2﹣4的对称轴上,则点M的坐标可能是( )
A.(1,0)B.(3,5)C.(﹣3,﹣4)D.(0,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
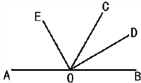
【题目】如图,点O在直线AB上,OE、OD分别是∠AOC、∠BOC的平分线.
(1)∠AOE的补角是∠____;∠BOD的余角是______;
(2)若∠AOC=118°,求∠COD的度数;
(3)射线OD与OE之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在△ABC中,点O是∠ABC和∠ACB的平分线的交点,若∠A=α,则∠BOC=90°+![]() ;如图②,∠CBO=
;如图②,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC=__________(用α表示);
∠ACB,∠A=α,则∠BOC=__________(用α表示);
(2)如图③,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC=__________(用α表示).
∠ECB,∠A=α,请猜想∠BOC=__________(用α表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com