
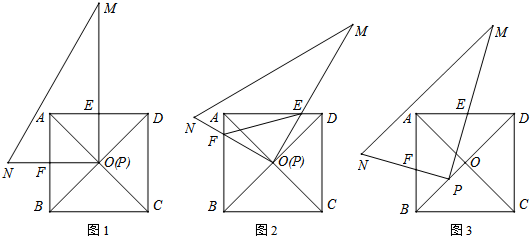
分析 (1)根据正方形的性质和角平分线的性质解答即可;
(2)①根据正方形的性质和旋转的性质证明△FOA≌△EOD,得到答案;
②作OG⊥AB于G,根据余弦的概念求出OF的长,根据勾股定理求值即可;
③过点P作HP⊥BD交AB于点H,根据相似三角形的判定和性质求出PE与PF的数量关系,根据解答结果总结规律得到当BD=m•BP时,PE与PF的数量关系.
解答 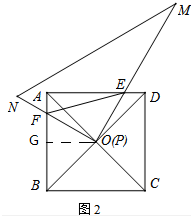 解:(1)PE=PF,理由:
解:(1)PE=PF,理由:
∵四边形ABCD为正方形,
∴∠BAC=∠DAC,又PM⊥AD、PN⊥AB,
∴PE=PF;
(2)①成立,理由:
∵AC、BD是正方形ABCD的对角线,
∴OA=OD,∠FAO=∠EDO=45°,∠AOD=90°,
∴∠DOE+∠AOE=90°,
∵∠MPN=90°,
∴∠FOA+∠AOE=90°,
∴∠FOA=∠DOE,
在△FOA和△EOD中,
$\left\{\begin{array}{l}{∠FAO=∠EDO}\\{OA=OD}\\{∠FOA=∠DOE}\end{array}\right.$,
∴△FOA≌△EOD,
∴OE=OF,即PE=PF;
②作OG⊥AB于G,
∵∠DOM=15°,
∴∠AOF=15°,则∠FOG=30°,
∵cos∠FOG=$\frac{OG}{OF}$,
∴OF=$\frac{1}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{3}}{3}$,又OE=OF,
∴EF=$\frac{2\sqrt{6}}{3}$;
③PE=2PF,
证明:如图3,过点P作HP⊥BD交AB于点H,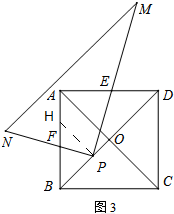
则△HPB为等腰直角三角形,∠HPD=90°,
∴HP=BP,
∵BD=3BP,
∴PD=2BP,
∴PD=2 HP,
又∵∠HPF+∠HPE=90°,∠DPE+∠HPE=90°,
∴∠HPF=∠DPE,
又∵∠BHP=∠EDP=45°,
∴△PHF∽△PDE,
∴$\frac{PF}{PE}$=$\frac{PH}{PD}$=$\frac{1}{2}$,
即PE=2PF,
由此规律可知,当BD=m•BP时,PE=(m-1)•PF.
点评 本题考查的是正方形的性质和旋转变换,掌握旋转变换的性质、找准对应关系正确运用三角形全等和相似的判定和性质定理是解题的关键,正确作出辅助线是解答本题的重点.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{41}$ | C. | 4或$\sqrt{34}$ | D. | 4或$\sqrt{41}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)2=a2-2ab+b2 | B. | (a-b)2=a2-b2 | C. | (a+b)(-a+b)=b2-a2 | D. | (a+b)(-a-b)=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
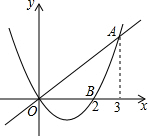 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | 0<x<3 | C. | 2<x<3 | D. | x<0或x>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
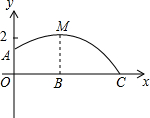 如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M,距地面4米高,球落地为C点.
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M,距地面4米高,球落地为C点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
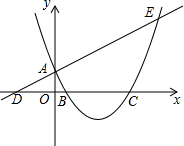 如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com