
分析 在原式前面加(2-1),利用两数的和与这两数的差的积,等于这两个数的平方差,把原式变成可以运用平方差公式的式子,再利用平方差公式计算即可.
解答 解:(2+1)(22+1)(24+1)(28+1)+1
=(2-1)(2+1)(22+1)(24+1)(28+1)+1,
=(22-1)(22+1)(24+1)(28+1)+1,
=(24-1)(24+1)(28+1)+1,
=(28-1)(28+1)+1,
=216-1+1,
因为216的末位数字是6,
所以原式末位数字是6.
故答案为:6.
点评 此题考查了尾数特征,关键在于添加因式(2-1)后构造成平方差公式结构,连续运用公式求解,另外掌握2的乘方的个位数的规律性循环也比较关键.


科目:初中数学 来源: 题型:解答题
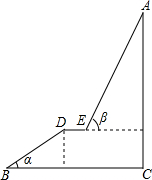 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
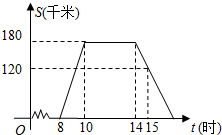 端午节三天假期的某一天,小明全家上午8时自架小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )
端午节三天假期的某一天,小明全家上午8时自架小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )| A. | 景点离小明家180千米 | B. | 小明到家的时间为17点 | ||
| C. | 返程的速度为60千米每小时 | D. | 10点至14点,汽车匀速行驶 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com