
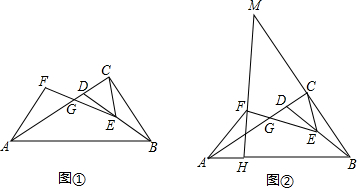
分析 (1)由直角三角形斜边上的中线性质得出CE=$\frac{1}{2}$BD=BE=DE,得出∠EBC=∠ECB=∠FAC,再证出∠CGE=∠ECB+∠CAB,即可得出结论;
(2)延长AF交BC的延长线于点T,延长BD交AT于N,连接NC、FC,先证出∠ANB=∠BCD=90°,再证明△TNC∽△TBA,得出∠TNC=∠CBA=∠CGE,证出N、F、E、C四点共圆,得出∠ENF=∠ECF=90°,证出FA=FC=FT,过T作TQ∥AB,交MH于点Q,则QT=AH=$\frac{1}{3}$BH,得出MQ=$\frac{1}{3}$MH,即可得出结论.
解答 (1)证明:∵∠ACB=90°,E是BD的中点,
∴CE=$\frac{1}{2}$BD=BE=DE,
∴∠EBC=∠ECB=∠FAC,
∵∠ECD=90°-ECB,∠CEG=∠ABC=90°-∠CAB,
∴在△CGE中,∠CGE=180°-∠ECD-∠CEG=∠ECB+∠CAB,
又∵∠FAB=∠FAC+∠CAB,
∴∠FAB=∠CGE;
(2)解:FM=2FH;理由如下:
延长AF交BC的延长线于点T,延长BD交AT于N,如图所示: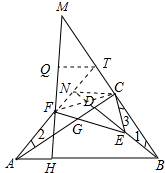 在△AND和△BCD中,∵∠1=∠2,∠NDA=∠CDB,
在△AND和△BCD中,∵∠1=∠2,∠NDA=∠CDB,
∴∠ANB=∠BCD=90°,即BN⊥AT,
连接NC、FC,
在Rt△TNB中,sin∠1=$\frac{TN}{TB}$,
在Rt△TCA中,sin∠2=$\frac{TC}{TA}$,
∴$\frac{TN}{TB}=\frac{TC}{TA}$,
∵∠NTC=∠BTA,
∴△TNC∽△TBA,
∴∠TNC=∠CBA=∠CGE,
∵∠TNC+∠CTE=90°,
∴四边形NCEF中,∠CEG+∠CNF=180°,
∴N、F、E、C四点共圆,
∴∠ENF=∠ECF=90°,
∴∠ACF=∠3=∠1=∠2,
∴FA=FC,
∵∠ATC+∠2=90°,∠TCF+∠ACF=90°,
∴∠ATC=∠TCF,
∴FT=FC=FA,
过T作TQ∥AB,交MH于点Q,
则QT=AH,
∴QT=AH=$\frac{1}{3}$BH,
∴MQ=$\frac{1}{3}$MH,
∴FM=2FH.
点评 本题考查了直角三角形斜边上的中线性质、三角函数、相似三角形的判定与性质、四点共圆、等腰三角形的判定等知识;本题难度较大,综合性强,特别是(2)中,需要作辅助线证明三角形相似、四点共圆、等腰三角形才能得出结论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16个 | B. | 20个 | C. | 25个 | D. | 30个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
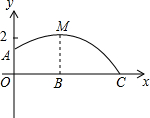 如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M,距地面4米高,球落地为C点.
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M,距地面4米高,球落地为C点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | -7 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -9 | B. | 9 | C. | 5 | D. | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )
某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )| A. | 每月阅读数量的平均数是50 | B. | 众数是42 | ||
| C. | 中位数是58 | D. | 每月阅读数量超过40的有4个月 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com