
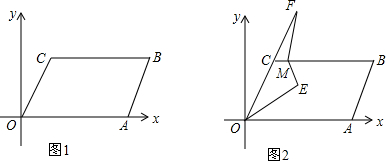
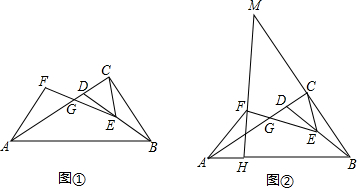
���� ��1����ͼ1����C��B�ֱ���CE��OA��E��BF��OA��F�����ı���OABC��ƽ���ı��Σ��õ�OC��AB��BC��OA��OC=AB��֤�á�OCE=��BAF���Ƴ���COE�ա�BAF���ɵõ������
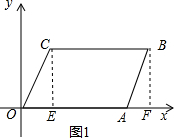
��2����ͼ2������P���߶�BC��ʱ������P��PM��OA��M������ֱ��OP��ƽ���ı���OABC������ֳ�1��3�����֣��õ�S��OPC=$\frac{1}{2}$CP•PM=$\frac{1}{3}$S�ı���OABC=$\frac{8}{3}$������ɵã���ͼ3������P���߶�AB��ʱ������P��PM��OA��M������ֱ��OP��ƽ���ı���OABC������ֳ�1��3�����֣��õ�S��OPC=$\frac{1}{2}$OA•PM=$\frac{1}{3}$S�ı���OABC=$\frac{8}{3}$�����ɵõ������
��3����ͼ4����E��EN��OA����EN��BC������ƽ���ߵ����ʵõ���MEN=��BME����NEO=��NEO�����EOA=x�㣬��BME=y��x+y=��E��2x+��F=y��Ȼ������x����ʾ��y���ٸ���2��E���F�������y��Ȼ����ݽ�ƽ���ߵĶ�����⼴�ɣ�
���  �⣺��1����ͼ1����C��B�ֱ���CE��OA��E��BF��OA��F��
�⣺��1����ͼ1����C��B�ֱ���CE��OA��E��BF��OA��F��
���ı���OABC��ƽ���ı��Σ�
��OC��AB��BC��OA��OC=AB��
���OCE=��BAF��
�ڡ�COE���BAF�У�
$\left\{\begin{array}{l}{��COE=��BAF}\\{��CEO=��BFA=90��}\\{OC=AB}\end{array}\right.$��
���COE�ա�BAF��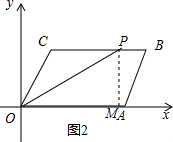
��BF=CE��AF=OE��
��A��4��0����C��1��2��
��B��5��2����
��S�ı���OABC=OA•CE=4��2=8��
��2����ͼ2������P���߶�BC��ʱ��
����P��PM��OA��M��
��ֱ��OP��ƽ���ı���OABC������ֳ�1��3�����֣�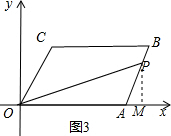
��S��OPC=$\frac{1}{2}$CP•PM=$\frac{1}{3}$S�ı���OABC=$\frac{8}{3}$��
��PC=$\frac{8}{3}$��
��P��$\frac{11}{3}$��2����
��ͼ3������P���߶�AB��ʱ��
����P��PM��OA��M��
��ֱ��OP��ƽ���ı���OABC������ֳ�1��3�����֣�
��S��OPC=$\frac{1}{2}$OA•PM=$\frac{1}{3}$S�ı���OABC=$\frac{8}{3}$��
��PM=$\frac{4}{3}$��
��ֱ��AB�Ľ���ʽΪy=2x-8��
�൱y=$\frac{4}{3}$ʱ��x=$\frac{28}{6}$��
��P��$\frac{28}{6}$��$\frac{4}{3}$����
����������P��$\frac{11}{3}$��2������$\frac{28}{6}$��$\frac{4}{3}$����
��3����ͼ4����E��EN��OA����EN��BC��
���MEN=��BME����NEO=��NEO��
���EOA=x�㣬��BME=y�㣬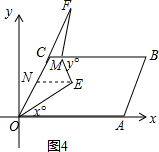
��x+y=��E��2x+��F=y��
����x�ã�3y=2��E+��F��
��2��E���F������
��2��E+��F=180�㣬
��3y=180�㣬
���y=60�㣬
��MBƽ�֡�FME��
���FME=2y=2��60��=120�㣮
���� ���⿼���˸���ͼ���������꣬�������ε������ƽ���ߵ����ʣ������ε�һ����ǵ������������ڵ������ڽǵĺ͵����ʣ���ƽ���ߵĶ��壬������Ŀ�����յ���ƽ�����ǽ���Ĺؼ���ȷʶͼ����ͼ�и��Ƕ�֮��Ĺ�ϵҲ����Ҫ��


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
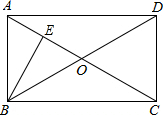 ��ͼ���ھ���ABCD�У�BC=40cm���Խ���BD��AB��20cm��BE��AC�ڵ�E����BE�ij���
��ͼ���ھ���ABCD�У�BC=40cm���Խ���BD��AB��20cm��BE��AC�ڵ�E����BE�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A��-1��0�����Գ���Ϊֱ��x=1����y��Ľ���B�ڣ�0��2���ͣ�0��3��֮�䣨���������㣩�����н��ۣ�
��ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A��-1��0�����Գ���Ϊֱ��x=1����y��Ľ���B�ڣ�0��2���ͣ�0��3��֮�䣨���������㣩�����н��ۣ�| A�� | �٢ۢ� | B�� | �٢ڢ� | C�� | �٢ڢ� | D�� | �٢ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
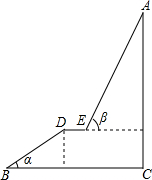 ��ͼ��AΪij���ξ�������ѹ۾��㣬�οͿɴ�B�������³��ȵ���С�۾�ƽ̨DE�۾���Ȼ������E�����������³�����A��������ʱ��A��������������ֱ�ӵ���C������֪��AC��BC��C��DE��BC��BC=110�ף�DE=9�ף�BD=60�ף���=32�㣬��=68�㣬��AC�ĸ߶ȣ����ο����ݣ�sin32���0.53��cos32���0.85��tan32���0.62��sin68���0.93��cos68���0.37��tan68���2.48��
��ͼ��AΪij���ξ�������ѹ۾��㣬�οͿɴ�B�������³��ȵ���С�۾�ƽ̨DE�۾���Ȼ������E�����������³�����A��������ʱ��A��������������ֱ�ӵ���C������֪��AC��BC��C��DE��BC��BC=110�ף�DE=9�ף�BD=60�ף���=32�㣬��=68�㣬��AC�ĸ߶ȣ����ο����ݣ�sin32���0.53��cos32���0.85��tan32���0.62��sin68���0.93��cos68���0.37��tan68���2.48���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com