
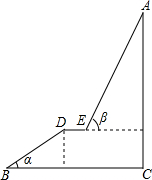
 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48) 分析 根据已知和余弦的概念求出DF的长,得到CG的长,根据正切的概念求出AG的长,求和得到答案.
解答 解:∵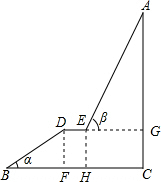 cos∠DBF=$\frac{BF}{BD}$,
cos∠DBF=$\frac{BF}{BD}$,
∴BF=60×0.85=51,
FH=DE=9,
∴EG=HC=110-51-9=50,
∵tan∠AEG=$\frac{AG}{EG}$,
∴AG=50×2.48=124,
∵sin∠DBF=$\frac{DF}{BD}$,
∴DF=60×0.53=31.8,
∴CG=31.8,
∴AC=AG+CG=124+31.8=155.8米.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念和坡角的概念是解题的关键,解答时注意:正确作出辅助线构造直角三角形准确运用锐角三角函数的概念列出算式.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E为AD上一点,将△ABE沿直线BE折叠,使点A落在BD上的点G处,延长EG交BC于点F.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E为AD上一点,将△ABE沿直线BE折叠,使点A落在BD上的点G处,延长EG交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{41}$ | C. | 4或$\sqrt{34}$ | D. | 4或$\sqrt{41}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | -7 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com