
分析 (1)设购买甲种鱼苗x尾,乙种鱼苗y尾,根据题意列一元一次方程组求解即可;
(2)设购买甲种鱼苗z尾,乙种鱼苗(700-z)尾,根据题意列不等式求出解集即可;
(3)设甲种鱼苗购买m尾,购买鱼苗的费用为w元,列出w与x之间的函数关系式,运用一次函数的性质解决问题.
解答 解:(1)设购买甲种鱼苗x尾,乙种鱼苗y尾,根据题意可得:
$\left\{\begin{array}{l}{x+y=700}\\{3x+5y=2500}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=500}\\{y=200}\end{array}\right.$.
答:购买甲种鱼苗500尾,乙种鱼苗200尾.
(2)设购买甲种鱼苗z尾,乙种鱼苗(700-z)尾,列不等式得:
85%z+90%(700-z)≥700×88%,
解得:z≤280.
答:甲种鱼苗至多购买280尾.
(3)设甲种鱼苗购买m尾,购买鱼苗的费用为w元,则
w=3m+5(700-m)=-2m+3500,
∵-2<0,
∴w随m的增大而减小,
∵0<m≤280,
∴当m=280时,w有最小值,w的最小值=3500-2×280=2940(元),
∴700-m=420.
答:当选购甲种鱼苗280尾,乙种鱼苗420尾时,总费用最低,最低费用为2940元.
点评 本题主要考查了二元一次方程组、一元一次不等式以及一次函数应用问题,审清题意,找到等量或不等关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
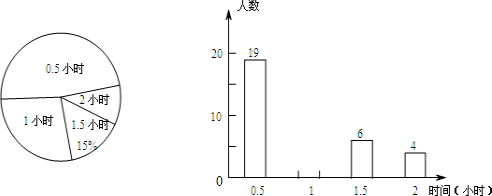
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
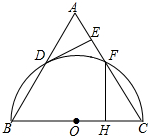 如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
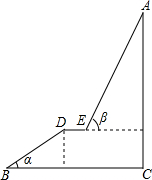 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
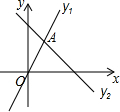 如图,两直线y2=-x+3与y1=2x相交于点A,下列错误的是( )
如图,两直线y2=-x+3与y1=2x相交于点A,下列错误的是( )| A. | x<3时,y1-y2>3 | B. | 当y1>y2时,x>1 | ||
| C. | y1>0且y2>0时,0<x<3 | D. | x<0时,y1<0且y2>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
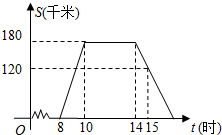 端午节三天假期的某一天,小明全家上午8时自架小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )
端午节三天假期的某一天,小明全家上午8时自架小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )| A. | 景点离小明家180千米 | B. | 小明到家的时间为17点 | ||
| C. | 返程的速度为60千米每小时 | D. | 10点至14点,汽车匀速行驶 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com