
 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E为AD上一点,将△ABE沿直线BE折叠,使点A落在BD上的点G处,延长EG交BC于点F.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E为AD上一点,将△ABE沿直线BE折叠,使点A落在BD上的点G处,延长EG交BC于点F.分析 (1)根据折叠的性质可得AE=EG,然后根据∠EGD=90°,可得ED>EG=AE,可得E不可能是AD中点;
(2)①根据折叠的性质,可得∠BGE=∠BAD=90°,根据平行四边形的性质可得∠BDC=∠BGF=90°,又AD∥BC,得出∠ADB=∠CBD,继而可证明△ABD∽△DCB;
②根据相似三角形对应边成比例以及勾股定理得知识,可证明a2+b2=ac.
解答 解:(1)不可以,由折叠可得,AE=EG.
在Rt△DEG中,ED>EG,即ED>AE.
∴E不可能是AD中点;
(2)①∵点A折叠到点G,
∴∠BGE=∠BAD=90°,
∵四边形EFCD为平行四边形,
∴∠BDC=∠BGF=90°,
又∵AD∥BC,
∴∠ADB=∠CBD,
∴△ABD∽△DCB;
②∵△ABD∽△DCB,
∴$\frac{AD}{BD}=\frac{BD}{CB}$,
∴BD2=AD•CB=ac,
又∵△ABD为Rt△ABD,
∴BD2=AD2+AB2=a2+b2,
∴a2+b2=ac.
点评 本题考查了四边形综合题,涉及了相似三角形的性质与判定,平行四边形的性质,折叠的性质,综合性较强,难度较大,需仔细分析,认真研究,结合图形理清题目边长之间的关系是解题的关键,本题对同学们的能力要求较高.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
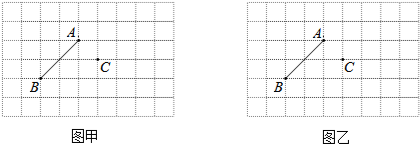
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
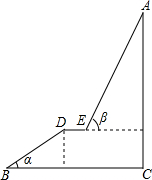 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com