
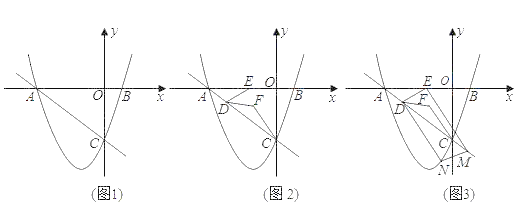
【题目】已知:在平面直角坐标系中,点O为坐标原点,直线y=﹣![]() x+b与x轴交于点A,与y轴交于点C.经过点A,C的抛物线y=ax2+3ax﹣3与x轴的另一个交点为点B.
x+b与x轴交于点A,与y轴交于点C.经过点A,C的抛物线y=ax2+3ax﹣3与x轴的另一个交点为点B.
(1)如图1,求a的值;
(2)如图2,点D,E分别在线段AC,AB上,且BE=2AD,连接DE,将线段DE绕点D顺时针旋转得到线段DF,且旋转角∠EDF=∠OAC,连接CF,求tan∠ACF的值;
(3)如图3,在(2)的条件下,当∠DFC=135°时,在线段AC的延长线上取点M,过点M作MN∥DE交抛物线于点N,连接DN,EM,若MN=DF,求点N的横坐标.
【答案】(1)a=![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)求出点A(﹣4,0),将点A的坐标代入二次函数表达式,即可求解;
(2)证明△ADE≌△GFD,即可求解;
(3)证明△DET≌△MSN(AAS),则MS=DT=![]() ,NS=ET=
,NS=ET=![]() ,设点M(x,﹣
,设点M(x,﹣![]() x﹣3),则点N(x﹣
x﹣3),则点N(x﹣![]() ,
,![]() ),将点N的坐标代入二次函数表达式,即可求解.
),将点N的坐标代入二次函数表达式,即可求解.
解:(1)y=ax2+3ax﹣3,当x=0,y=﹣3,故点C(0,﹣3),
将点C的坐标代入直线表达式并解得:b=﹣3,
则直线AC的表达式为:y=﹣![]() x﹣3,则点A(﹣4,0),
x﹣3,则点A(﹣4,0),
将点A的坐标代入二次函数表达式并解得:a=![]() ;
;
(2)在直线AC上取点G使DG=AE,连接FG,过点F作FH⊥AC,
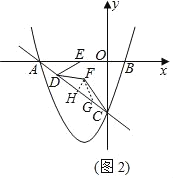
∵∠FDC+∠FDE=∠BAC+∠AED,而∠BAC=∠EDF,
∴∠FDH=∠AED,
而DG=AE,DF=DE,
∴△ADE≌△GFD,
∴AD=GF,
∵AB=AC=5,BE=2AD,
∴AD=GF=CG,
∵tan∠BAC=![]() ,设FH=3m,则HG=4m,FG=5m=GC,
,设FH=3m,则HG=4m,FG=5m=GC,
tan∠ACF=![]() ;
;
(3)如图3,过点D作DR⊥FC交FC的延长线于点R,过点F作FH⊥CD交于点H,
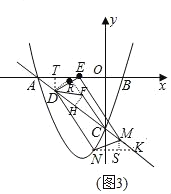
由(2)知tan∠ACF=![]() ,
,
在Rt△CDR中,设DR=![]() t,则CR=3
t,则CR=3![]() t,CD=10t,
t,CD=10t,
∵∠DFC=135°,则△DFR是等腰直角三角形,则FR=DR=![]() t,
t,
CF=CR﹣CF=2![]() t,
t,
在Rt△FHC中,tan∠ACF=![]() ,
,
则FH=2t,CH=6t,DH=CD﹣CH=10t﹣6t=4t,
则tan∠FDH=![]() =tan∠AED,
=tan∠AED,
在Rt△ADT中,tan∠BAC=![]() ,
,
设:DT=3n,则AT=4n,AD=5n,
在Rt△DTE中,tan∠AED=![]() ,
,
则ET=2DT=6n,BE=2AD=10n,
∵AT+TE+BE=AB,即4n+6n+10n=5,
解得:n=![]() ,
,
则ET=![]() ,DT=
,DT=![]() ;
;
∵MN=EF=DE,且MN∥DE,
∴四边形MNDE为平行四边形,∴∠DEM=∠DNM,
过点N作x轴的平行线交直线AC于点K,过点M作MS⊥NK于点S,
则∠AEM=∠KND,∴∠TED=∠MNS,
而MN=DE,∠ETD=∠MSN=90°,
∴△DET≌△MSN(AAS),
∴MS=DT=![]() ,NS=ET=
,NS=ET=![]() ,
,
设点M(x,﹣![]() x﹣3),则点N(x﹣
x﹣3),则点N(x﹣![]() ,
,![]() ),
),
将点N的坐标代入二次函数表达式得:
![]()
解得:![]() (舍去负值),
(舍去负值),
故点N的横坐标为:![]() .
.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的
一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运
动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为
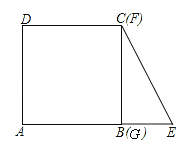
A.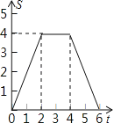 B.
B.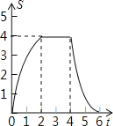
C.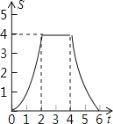 D.
D.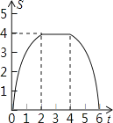
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则BG的长为( )
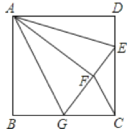
A. 1B. 2C. 1.5D. 2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对学生进行革命传统教育,红旗中学开展了“清明节祭扫”活动.全校学生从学校同时出发,步行![]() 米到达烈士纪念馆.学校要求九
米到达烈士纪念馆.学校要求九![]() 班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的
班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的![]() 倍,结果比其他班提前
倍,结果比其他班提前![]() 分钟到达.分别求九(1)班、其他班步行的平均速度.
分钟到达.分别求九(1)班、其他班步行的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,![]() .将△ABC绕点A逆时针旋转60°,得到△AB'C'(点B,C的对应点分别为点B′,C′),延长C′B′分别交AC,BC于点D,E,若DE=2,则AD的长为_____.
.将△ABC绕点A逆时针旋转60°,得到△AB'C'(点B,C的对应点分别为点B′,C′),延长C′B′分别交AC,BC于点D,E,若DE=2,则AD的长为_____.
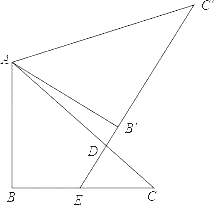
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大以来,某校已举办五届校园艺术节.为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
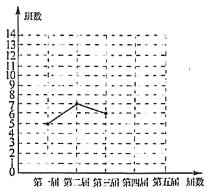
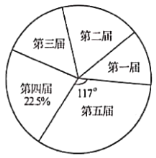
(1)五届艺术节共有________个班级表演这些节日,班数的中位数为________,在扇形统计图中,第四届班级数的扇形圆心角的度数为________;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示).利用树状图或表格求出该班选择
表示).利用树状图或表格求出该班选择![]() 和
和![]() 两项的概率.
两项的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形AOBC中,对角线交于点E,双曲线y=![]() (k>0)经过A、E两点,若平行四边形AOBC的面积为24,则k的值是( )
(k>0)经过A、E两点,若平行四边形AOBC的面积为24,则k的值是( )
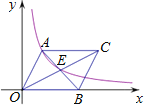
A. 8B. 7.5C. 6D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且AB=1,OB=![]() ,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
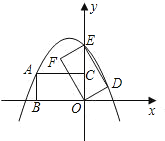
(1)判断点E是否在y轴上,并说明理由;
(2)求抛物线的函数表达式;
(3)在x轴的上方是否存在点P,点Q,使以点O,B,P,Q为顶点的平行四边形的面积是矩形ABOC面积的2倍,且点P在抛物线上?若存在,请求出点P,点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com