
【题目】如图所示,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且AB=1,OB=![]() ,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
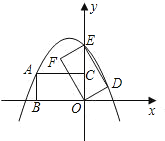
(1)判断点E是否在y轴上,并说明理由;
(2)求抛物线的函数表达式;
(3)在x轴的上方是否存在点P,点Q,使以点O,B,P,Q为顶点的平行四边形的面积是矩形ABOC面积的2倍,且点P在抛物线上?若存在,请求出点P,点Q的坐标;若不存在,请说明理由.
【答案】(1)在;(2)![]() ;(3)当点P1的坐标为(0,2)时,点Q的坐标分别为Q1(-
;(3)当点P1的坐标为(0,2)时,点Q的坐标分别为Q1(-![]() ,2),Q2(
,2),Q2(![]() ,2);当点P2的坐标为(-
,2);当点P2的坐标为(-![]() ,2)时,点Q的坐标分别为Q3(-
,2)时,点Q的坐标分别为Q3(-![]() ,2),Q4(
,2),Q4(![]() ,2).
,2).
【解析】
(1)可连接OA,通过证∠AOE=60°,即与旋转角相同来得出OE在y轴上的结论.
(2)已知了AB,OB的长即可求出A的坐标,在直角三角形OEF中,可用勾股定理求出OE的长,也就能求得E点的坐标,要想得出抛物线的解析式还少D点的坐标,可过D作x轴的垂线,通过构建直角三角形,根据OD的长和∠DOx的正弦和余弦值来求出D的坐标.
求出A、E、D三点坐标后即可用待定系数法求出抛物线的解析式.
(3)可先求出矩形的面积,进而可得出平行四边形OBPQ的面积.由于平行四边形中OB边的长是定值,因此可根据平行四边形的面积求出P点的纵坐标(由于P点在x轴上方,因此P的纵坐标为正数),然后将P点的纵坐标代入抛物线中可求出P点的坐标.求出P点的坐标后,将P点分别向左、向右平移OB个单位即可得出Q点的坐标,由此可得出符合条件的两个P点坐标和四个Q点坐标.
(1)点E在y轴上
理由如下:
连接AO,如图所示,在Rt△ABO中,∵AB=1,BO=![]() ,
,
∴AO=2∴sin∠AOB=![]() ,∴∠AOB=30°
,∴∠AOB=30°
由题意可知:∠AOE=60°∴∠BOE=∠AOB+∠AOE=30°+60°=90°
∵点B在x轴上,∴点E在y轴上.
(2)过点D作DM⊥x轴于点M,
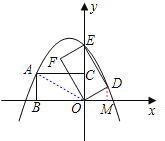
∵OD=1,∠DOM=30°
∴在Rt△DOM中,DM=![]() ,OM=
,OM=![]()
∵点D在第一象限,
∴点D的坐标为(![]() ,
,![]() )
)
由(1)知EO=AO=2,点E在y轴的正半轴上
∴点E的坐标为(0,2)
∴点A的坐标为(-![]() ,1)
,1)
∵抛物线y=ax2+bx+c经过点E,
∴c=2
由题意,将A(-![]() ,1),D(
,1),D(![]() ,
,![]() )代入y=ax2+bx+2中,
)代入y=ax2+bx+2中,
得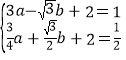
解得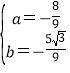
∴所求抛物线表达式为:y=-![]() x2-
x2-![]() x+2
x+2
(3)存在符合条件的点P,点Q.
理由如下:∵矩形ABOC的面积=ABBO=![]()
∴以O,B,P,Q为顶点的平行四边形面积为2![]() .
.
由题意可知OB为此平行四边形一边,
又∵OB=![]()
∴OB边上的高为2
依题意设点P的坐标为(m,2)
∵点P在抛物线y=-![]() x2-
x2-![]() x+2上
x+2上
∴-![]() m2-
m2-![]() m+2=2
m+2=2
解得,m1=0,m2=-![]()
∴P1(0,2),P2(-![]() ,2)
,2)
∵以O,B,P,Q为顶点的四边形是平行四边形,
∴PQ∥OB,PQ=OB=![]() ,
,
∴当点P1的坐标为(0,2)时,点Q的坐标分别为Q1(-![]() ,2),Q2(
,2),Q2(![]() ,2);
,2);
当点P2的坐标为(-![]() ,2)时,点Q的坐标分别为Q3(-
,2)时,点Q的坐标分别为Q3(-![]() ,2),Q4(
,2),Q4(![]() ,2).
,2).


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】如图,已知⊙O为△ABC(∠A<∠ABC)的外接圆,且AB为![]() 的直径,AB=8,点D为AB延长线上一点,点 E为半径OB上一点,连接CD、CE、OC,且∠BCD=∠A.
的直径,AB=8,点D为AB延长线上一点,点 E为半径OB上一点,连接CD、CE、OC,且∠BCD=∠A.

(1)求证:CD为![]() 的切线;
的切线;
(2)若CB=CE,求证:CE2=CO2-OA·OE;
(3)在(2)的条件下,求OE+BC的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
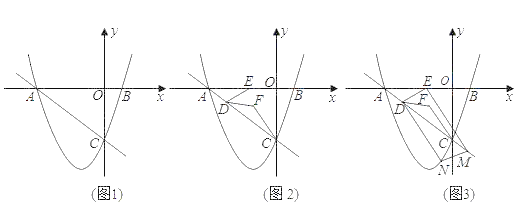
【题目】已知:在平面直角坐标系中,点O为坐标原点,直线y=﹣![]() x+b与x轴交于点A,与y轴交于点C.经过点A,C的抛物线y=ax2+3ax﹣3与x轴的另一个交点为点B.
x+b与x轴交于点A,与y轴交于点C.经过点A,C的抛物线y=ax2+3ax﹣3与x轴的另一个交点为点B.
(1)如图1,求a的值;
(2)如图2,点D,E分别在线段AC,AB上,且BE=2AD,连接DE,将线段DE绕点D顺时针旋转得到线段DF,且旋转角∠EDF=∠OAC,连接CF,求tan∠ACF的值;
(3)如图3,在(2)的条件下,当∠DFC=135°时,在线段AC的延长线上取点M,过点M作MN∥DE交抛物线于点N,连接DN,EM,若MN=DF,求点N的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
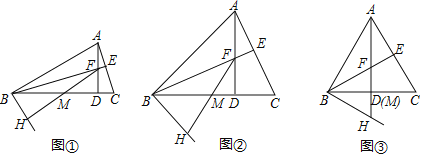
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.
填空:线段AD,BE之间的关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.
(3)解决问题
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知双曲线![]() 与直线
与直线![]() 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线![]() 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线![]() 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
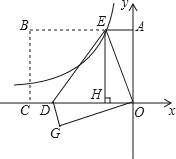
【题目】如图,在直角坐标系中,矩形OABC的顶点C在x轴的负半轴上,点A在y轴正半轴上,矩形OABC的面积为8![]() .把矩形OABC沿DE翻折,使点B与点O重合,点C落在第三象限的G点处,作EH⊥x轴于H,过E点的反比例函数y=
.把矩形OABC沿DE翻折,使点B与点O重合,点C落在第三象限的G点处,作EH⊥x轴于H,过E点的反比例函数y=![]() 图象恰好过DE的中点F.则k=_____,线段EH的长为:_____.
图象恰好过DE的中点F.则k=_____,线段EH的长为:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店购进甲、乙两种图书共100本,甲、乙两种图书的进价分别为每本15元、35元,甲、乙两种图书的售价分别为每本20元、45元.
(1)若书店购书恰好用了2300元,求购进的甲、乙图书各多少本?
(2)销售时,甲图书打8.5折,乙图书不打折.若甲、乙两种图书全部销售完后共获利![]() ,求购进的甲、乙图书各多少本?
,求购进的甲、乙图书各多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(1)如图①所示,若![]() ,求证:
,求证:![]() ;
;
(2)如图②所示,若![]() ,如图③所示,若
,如图③所示,若![]() (点
(点![]() 与点
与点![]() 重合),猜想线段
重合),猜想线段![]() 、
、![]() 与
与![]() 之间又有怎样的数量关系?请直接写出你的猜想,不需证明.
之间又有怎样的数量关系?请直接写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:a*b=![]() ,则下列等式中对于任意实数 a、b、c 都成立的是( )
,则下列等式中对于任意实数 a、b、c 都成立的是( )
①a+(b*c)=(a+b)*(a+c) ②a*(b+c)=(a+b)*c
③a*(b+c)=(a*b)+(a*c) ④(a*b)+c= ![]() +(b*2c)
+(b*2c)
A. ①②③ B. ①②④ C. ①③④ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com