
【题目】(1)按要求将下列几何体进行分类,并将分类后几何体的名称写在对应的括号内.

柱体:{ …}
锥体:{ …}
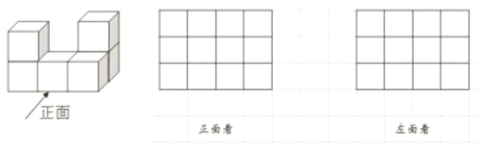
(2)6个完全相同的正方体组成如图所示的几何体,画出该几何体从正面,左面看到的形状图(用阴影画在所给的方格中)
科目:初中数学 来源: 题型:
【题目】若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=﹣![]() 图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
A.x1<x2<x3 B.x1<x3<x2
C.x2<x1<x3 D.x2<x3<x1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的高线,在BC边上截取点E,使得CE=BD,过E作EF∥AB,过C作CP⊥BC交EF于点P。过B作BM⊥AC于M,连接EM、PM。
(1)依题意补全图形;
(2)若AD=DC,探究EM与PM的数量关系与位置关系,并加以证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
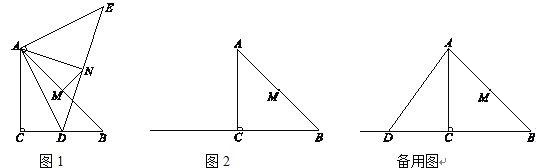
【题目】在△ABC中,∠ACB=90°,AC=BC=4,M为AB的中点.D是射线BC上一个动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED,N为ED的中点,连接AN,MN.
(1)如图1,当BD=2时,AN=___ __,NM与AB的位置关系是____ _____;
(2)当4<BD<8时,
①依题意补全图2;
②判断(1)中NM与AB的位置关系是否发生变化,并证明你的结论;
(3)连接ME,在点D运动的过程中,当BD的长为何值时,ME的长最小?最小值是多少?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2
(1)求实数k的取值范围。
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种产品,每件产品的成本为2400元,销售单价定位3000元,该商场为了促销,规定客户一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元;
(1)设一次购买这种产品x(x≥10)件,商场所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
(2)在客户购买产品的件数尽可能少的前提下,商场所获的利润为12000元,此时该商场销售了多少件产品?
(3)填空:该商场的销售人员发现,当客户一次购买产品的件数在某一个区间时,会出现随着一次购买的数量的增多,商场所获的利润反而减少这一情况,客户一次购买产品的数量x满足的条件是 (其它销售条件不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
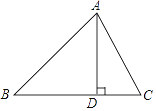
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路:
作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,列出方程求出x→再求出AD的长,从而计算三角形的面积.请你按照他们的解题思路完成解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE=![]() ∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是_____.
∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°AB=AC,分别过点B、C做经过点A的直线的垂线BD、CE,若BD=14cm,CE=3cm,则DE=_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com