
【题目】如图,AD是△ABC的高线,在BC边上截取点E,使得CE=BD,过E作EF∥AB,过C作CP⊥BC交EF于点P。过B作BM⊥AC于M,连接EM、PM。
(1)依题意补全图形;
(2)若AD=DC,探究EM与PM的数量关系与位置关系,并加以证明。

【答案】(1)见解析;(2)EM⊥PM,EM=PM,证明见解析.
【解析】
(1)根据要求画出图形即可;
(2)连接MD,证明△ABD≌△PEC,则AD=PC,可得出PC=DC,再证△DCM≌△PCM,则MD=MP,∠PMC=∠DMC,再证△MDB≌△MEC,则MD=ME,∠BMD=∠CME,即可得出EM与PM的数量关系与位置关系.
解:(1)补全的图形如图所示;
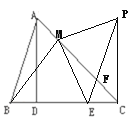
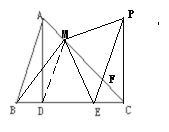
(2)EM⊥PM,EM=PM.
证明:连接DM,∵EF∥AB,∴∠ABD=∠PEC,
∵AD是△ABC的高线,CP⊥BC,
∴∠ADB=∠PCE=90°,
∵BD=EC,
∴△ABD≌△PEC,
∴AD=PC,
∵AD=DC,
∴PC=DC,
∵AD是△ABC的高线,CP⊥BC,AD=DC,
∴∠ACD=∠ACP=45°,
又∵CM=CM,
∴△DCM≌△PCM,
∴MD=MP,∠PMC=∠DMC;
∵BM⊥AC,∠ACD=45°,
∴MB=MC,∠ACD=∠MBC=45°,
又∵BD=CE,
∴△MDB≌△MEC,
∴MD=ME,∠BMD=∠CME,
∴MP=ME;
∵BM⊥AC,
∴∠BMD +∠DMC=90°,
∵∠BMD=∠CME,∠PMC=∠DMC,
∴∠CME +∠PMC =90°,即MP⊥ME,
∴EM与PM的数量关系与位置关系是:EM⊥PM,EM=PM.


科目:初中数学 来源: 题型:
【题目】小明租用共享单车从家出发,匀速骑行到相距![]() 米的图书馆还书.小明出发的同时,他的爸爸以每分钟
米的图书馆还书.小明出发的同时,他的爸爸以每分钟![]() 米的速度从图书馆沿同一条道路步行回家,小明在图书馆停留了
米的速度从图书馆沿同一条道路步行回家,小明在图书馆停留了![]() 分钟后沿原路按原速返回.设他们出发后经过
分钟后沿原路按原速返回.设他们出发后经过![]() (分)时,小明与家之间的距离为
(分)时,小明与家之间的距离为![]() (米),小明爸爸与家之间的距离为
(米),小明爸爸与家之间的距离为![]() (米),图中折线
(米),图中折线![]() 、线段
、线段![]() 分别表示
分别表示![]() 、
、![]() 与
与![]() 之间的函数关系的图象.小明从家出发,经过___分钟在返回途中追上爸爸.
之间的函数关系的图象.小明从家出发,经过___分钟在返回途中追上爸爸.
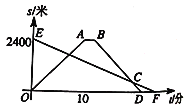
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是 _____________ ,(证明你的结论. )
(2)当四边形ABCD的对角线满足 __________条件时,四边形EFGH是矩形(不用证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
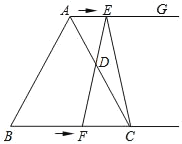
(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形;
(2)填空:①当t为 s时,四边形ACFE是菱形;②当t为 s时,△ACE的面积是△ACF的面积的2倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生整体的数学学习能力,年级组织了“数学钻石活动”,从中随机抽取部分学生的成绩进行统计分析,整理得到如下不完整的频数分布表和数分布直方图:


(1)表中的![]() ,
,![]() ;
;
(2)把上面的频数分布直方图补充完整;
(3)根据调查结果,估计年级500名学生中,成绩不低于85分的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在反比例函数
在反比例函数![]() 的第一象限内的图像上,
的第一象限内的图像上,![]() ,
,![]() ,动点
,动点![]() 在
在![]() 轴的上方,且满足
轴的上方,且满足![]() .
.
(1)若点![]() 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,求
,求![]() 的最小值;
的最小值;
(3)若点![]() 是平面内一点,使得以
是平面内一点,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,则请你直接写出满足条件的所有点
为顶点的四边形是菱形,则请你直接写出满足条件的所有点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形 ABCD 绕点 A 按逆时针方向旋转到正方形AB ' C ' D ' ,旋转角为 ( 0<< 180 ) ,连接 B ' D 、 C ' D ,若 B ' D C ' D ,则 =____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)按要求将下列几何体进行分类,并将分类后几何体的名称写在对应的括号内.

柱体:{ …}
锥体:{ …}
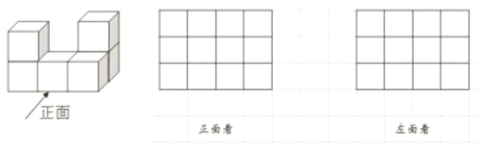
(2)6个完全相同的正方体组成如图所示的几何体,画出该几何体从正面,左面看到的形状图(用阴影画在所给的方格中)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com