
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是 _____________ ,(证明你的结论. )
(2)当四边形ABCD的对角线满足 __________条件时,四边形EFGH是矩形(不用证明)

【答案】(1)平行四边形;证明见解析(2)AC⊥BD
【解析】
(1)连接BD,根据三角形的中位线定理得到EH∥BD,EH=![]() BD,FG∥BD,FG=
BD,FG∥BD,FG=![]() BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形.
(1)四边形EFGH的形状是平行四边形.理由如下:
如图,连结BD,
∵E、H分别是AB、AD中点,
∴EH∥BD,EH=![]() BD,
BD,
同理FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
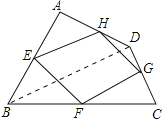
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
如图,连结AC、BD,
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形,
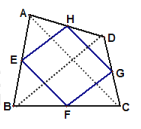
故答案为:AC⊥BD.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD与矩形EFGH在直线l的同侧,边AD,EH在直线l上,且AD=5cm,EH=4cm,EF=3cm.保持正方形ABCD不动,将矩形EFGH沿直线l左右移动,连接BF,CG,则BF+CG的最小值为_____________cm

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=﹣![]() 图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
A.x1<x2<x3 B.x1<x3<x2
C.x2<x1<x3 D.x2<x3<x1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,求证:
,求证:![]() ,请将证明过程填写完整.
,请将证明过程填写完整.
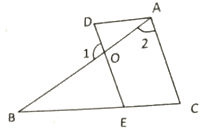
证明:∵![]() (已知)
(已知)
又∵![]() ( )
( )
∴________![]() ,
,
∴![]() ____________( )
____________( )
∴![]() ______________( )
______________( )
又∵![]() (已知)
(已知)
∴![]() ________________,
________________,
∴![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商店计划从厂家购进![]() 两种不同型号的电风扇,若购进8台
两种不同型号的电风扇,若购进8台![]() 型和20台
型和20台![]() 型电风扇,需资金7600元,若购进4台
型电风扇,需资金7600元,若购进4台![]() 型和15台
型和15台![]() 型电风扇,需资金5300元.
型电风扇,需资金5300元.
(1)求![]() 型电风扇每台的进价各是多少元;
型电风扇每台的进价各是多少元;
(2)该商店经理计划进这两种电风扇共50台,而可用于购买这两种电风扇的资金不超过12800元,根据市场调研,销售一台![]() 型电风扇可获利80元,销售一台
型电风扇可获利80元,销售一台![]() 型电风扇可获利120元.若两种电扇销售完时,所获得的利润不少于5000元.问有哪几种进货方案?哪种方案获得最大?最大利润是多少?
型电风扇可获利120元.若两种电扇销售完时,所获得的利润不少于5000元.问有哪几种进货方案?哪种方案获得最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的高线,在BC边上截取点E,使得CE=BD,过E作EF∥AB,过C作CP⊥BC交EF于点P。过B作BM⊥AC于M,连接EM、PM。
(1)依题意补全图形;
(2)若AD=DC,探究EM与PM的数量关系与位置关系,并加以证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路:
作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,列出方程求出x→再求出AD的长,从而计算三角形的面积.请你按照他们的解题思路完成解答过程.
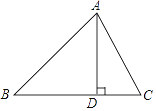
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com