
����Ŀ��С�����ù��������Ӽҳ������������е����![]() ��ͼ��ݻ��飮С��������ͬʱ�����İְ���ÿ����
��ͼ��ݻ��飮С��������ͬʱ�����İְ���ÿ����![]() ���ٶȴ�ͼ�����ͬһ����·���лؼң�С����ͼ���ͣ����
���ٶȴ�ͼ�����ͬһ����·���лؼң�С����ͼ���ͣ����![]() ���Ӻ���ԭ·��ԭ�ٷ��أ������dz�����
���Ӻ���ԭ·��ԭ�ٷ��أ������dz�����![]() ���֣�ʱ��С�����֮��ľ���Ϊ
���֣�ʱ��С�����֮��ľ���Ϊ![]() ���ף���С���ְ����֮��ľ���Ϊ
���ף���С���ְ����֮��ľ���Ϊ![]() ���ף���ͼ������
���ף���ͼ������![]() ���߶�
���߶�![]() �ֱ��ʾ
�ֱ��ʾ![]() ��
��![]() ��
��![]() ֮��ĺ�����ϵ��ͼ��С���Ӽҳ���������___�����ڷ���;���ϰְ֣�
֮��ĺ�����ϵ��ͼ��С���Ӽҳ���������___�����ڷ���;���ϰְ֣�
���𰸡�̽��һ����FDC+��ECD=180��+��A��̽��������DPC=90��+![]() ��A��̽��������DPC=
��A��̽��������DPC=![]() ����A+��B����̽���ģ���P=
����A+��B����̽���ģ���P=![]() ����A+��B+��E+��F��-180��.
����A+��B+��E+��F��-180��.
��������
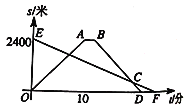
̽��һ�����������ε�һ����ǵ������������ڵ������ڽǵĺͿɵá�FDC=��A+��ACD����ECD=��A+��ADC���ٸ����������ڽǺͶ����������ɵý⣻
̽���������ݽ�ƽ���ߵĶ���ɵá�PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��ACD��Ȼ������������ڽǺͶ�����ʽ�������ɵý⣻
��ACD��Ȼ������������ڽǺͶ�����ʽ�������ɵý⣻
̽�����������ı��ε��ڽǺͶ�����ʾ����ADC+��BCD��Ȼ��ͬ��̽������ɣ�
̽���ģ����������ε��ڽǺ�ʽ��ʾ����EDC+��BCD��Ȼ��ͬ��̽������ɣ�
�⣺̽��һ���ߡ�FDC=��A+��ACD����ECD=��A+��ADC��
���FDC+��ECD=��A+��ACD+��A+��ADC=180��+��A��
̽��������DP��CP�ֱ�ƽ�֡�ADC�͡�ACD��
���PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��ACD��
��ACD��
���DPC=180��-��PDC-��PCD��
=180��-![]() ��ADC-
��ADC-![]() ��ACD��
��ACD��
=180��-![]() ����ADC+��ACD����
����ADC+��ACD����
=180��-![]() ��180��-��A����
��180��-��A����
=90��+![]() ��A��
��A��
̽��������DP��CP�ֱ�ƽ�֡�ADC�͡�BCD��
���PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��BCD��
��BCD��
���DPC=180��-��PDC-��PCD��
=180��-![]() ��ADC-
��ADC-![]() ��BCD��
��BCD��
=180��-![]() ����ADC+��BCD����
����ADC+��BCD����
=180��-![]() ��360��-��A-��B����
��360��-��A-��B����
=![]() ����A+��B����
����A+��B����
̽���ģ�������ABCDEF���ڽǺ�Ϊ����6-2��180��=720����
��DP��CP�ֱ�ƽ�֡�EDC�͡�BCD��
���PDC=![]() ��EDC����PCD=
��EDC����PCD=![]() ��BCD��
��BCD��
���P=180��-��PDC-��PCD
=180��-![]() ��EDC-
��EDC-![]() ��BCD
��BCD
=180��-![]() ����EDC+��BCD��
����EDC+��BCD��
=180��-![]() ��720��-��A-��B-��E-��F��
��720��-��A-��B-��E-��F��
=![]() ����A+��B+��E+��F��-180����
����A+��B+��E+��F��-180����
����P=![]() ����A+��B+��E+��F��-180����
����A+��B+��E+��F��-180����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ȤС�������һ����¥AB�ĸ߶ȣ���ͼ6����¥ǰ��һ��б��BC����֪BC�ij�Ϊ12�ף������¶�i=1��![]() ������C��40��D�����ò���Dz�ô�¥����A������Ϊ37�㣬�����DE�ĸ�Ϊ1.5�ף����¥AB�ĸ߶�ԼΪ�����ף��������ȷ��0.1�ף�
������C��40��D�����ò���Dz�ô�¥����A������Ϊ37�㣬�����DE�ĸ�Ϊ1.5�ף����¥AB�ĸ߶�ԼΪ�����ף��������ȷ��0.1�ף�
���ο����ݣ�sin37����0.60��cos37����0.80��tan37����0.75��![]() ��1.73����
��1.73����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̶�м�2017��ɹ�����ȫ����������֮����������ȫ���������У�ijС��������Ӧ��������С���ڰ�װ�����������ܰ��ʾ�ƺ������䣬������2����ܰ��ʾ�ƺ�3�������乲��550Ԫ����������ĵ�������ܰ��ʾ�Ƶ��۵�3����
��1������ܰ��ʾ�ƺ�������ĵ��۸��Ƕ���Ԫ��
��2����С��������Ҫ����48�������䣬���������ܰ��ʾ�ƺ������乲100�����ҷ��ò�����10000Ԫ�������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
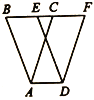
����Ŀ����ͼ���ڡ�ABC�У�![]() ������ABC��ÿ��2cm���ٶ���
������ABC��ÿ��2cm���ٶ���![]() ����ֱ������ƽ�ƣ�����ͼ�ζ�ӦΪ��DEF����ƽ��ʱ��Ϊt�룬��Ҫʹ
����ֱ������ƽ�ƣ�����ͼ�ζ�ӦΪ��DEF����ƽ��ʱ��Ϊt�룬��Ҫʹ![]() ��������
��������![]() ��ֵΪ_____�룮
��ֵΪ_____�룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¶���һ�������Σ�����ƽ���͵��ڵ�����ƽ����4���������ν�����̬�����Ρ����磺ij���������߳��ֱ���5��6��8����Ϊ![]() ����������������dz�̬�����Ρ�
����������������dz�̬�����Ρ�
��1������ABC���߳��ֱ���2��![]() ��4�����������_________��̬�����Σ�����������������������
��4�����������_________��̬�����Σ�����������������������
��2����Rt��ABC�dz�̬�����Σ���������ε����߳�֮��Ϊ__________________���밴��С�������У���
��3����ͼ��Rt��ABC�У���ACB=90�㣬BC=6����DΪAB���е㣬����CD������BCD�dz�̬�����Σ����ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�Ƶ�C˳ʱ����ת90���õ���EDC������A��D��E��ͬһ��ֱ���ϣ���ACB=20�������ADC�Ķ����ǣ�������
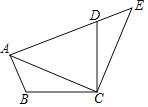
A. 55��B. 60��C. 65��D. 70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�����EFGH��ֱ��l��ͬ�࣬��AD��EH��ֱ��l�ϣ���AD=5cm��EH=4cm��EF=3cm������������ABCD������������EFGH��ֱ��l�����ƶ�������BF��CG����BF+CG����СֵΪ_____________cm

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣨x1��y1������x2��y2������x3��y3�����Ƿ���������y=��![]() ͼ���ϵĵ㣬����y1��0��y2��y3�������и�ʽ����ȷ���ǣ� ��
ͼ���ϵĵ㣬����y1��0��y2��y3�������и�ʽ����ȷ���ǣ� ��
A��x1��x2��x3 B��x1��x3��x2
C��x2��x1��x3 D��x2��x3��x1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD����ABC�ĸ��ߣ���BC���Ͻ�ȡ��E��ʹ��CE��BD����E��EF��AB����C��CP��BC��EF�ڵ�P����B��BM��AC��M������EM��PM��
(1)�����ⲹȫͼ�Σ�
(2)��AD��DC��̽��EM��PM��������ϵ��λ�ù�ϵ��������֤����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com