练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在Rt△ABC中，∠ACB=90°，CD为AB边上的高，若点A关于CD所在直线的对称点E恰好为AB的中点，则∠B的度数是（ ）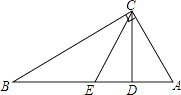

    A.60°
    B.45°
    C.30°
    D.75°

    【答案】C
    【解析】根据题意，在Rt△ABC中，∠ACB=90°，CD为AB边上的高，点A关于CD所在直线的对称点E恰好为AB的中点，可知∠CED=∠A，CE=BE=AE，由此可得∠ECA=∠A，∠B=∠BCE，判断出△ACE是等边三角形，得到∠CED=60°，从而根据等腰三角形的外角的性质得到∠B= ∠CED=30°．

    根据对称的性质点A关于CD所在直线的对称点E恰好为AB的中点，得到对应角、对应边相等，得到△ACE是等边三角形，根据等腰三角形的外角的性质得到∠B的度数.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，在△ABC中，∠BAC=90°，AB⊥AC，AB=3，BC=5，EF垂直平分BC，点P为直线EF上的任一点，则AP+BP的最小值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，AC=BC，BE是中线，CG平分∠ACB交BE于点G，F为AB边上一点，且∠ACF=∠CBG．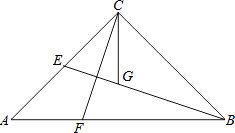

    （1）求证：CF=BG；
    （2）延长CG交AB于点H，判断点G是否在线段AB的垂直平分线上？并说明理由．
    （3）过点A作AD⊥AB交BE的延长线于点D，请证明：CF=2DE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在频数分布直方图中，各小长方形的高等于相应组的（　　）
    A.组距
    B.组数
    C.频数
    D.频率

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一块矩形铁皮的四个角各剪去一个边长为1米的正方形后，剩下的部分刚好围成一个容积为15m3的无盖长方体水箱，且此长方体水箱的底面长比宽多2米．求该矩形铁皮的长和宽各是多少米？若设该矩形铁皮的宽是x米，则根据题意可得方程为（ ）
    A.（x+2）（x﹣2）×1=15
    B.x（x﹣2）×1=15
    C.x（x+2）×1=15
    D.（x+4）（x﹣2）×1=15

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了抓住文化艺术节的商机，某商店决定购进A、B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，需要800元．

    （1）求购进A、B两种纪念品每件各需多少元？

    （2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不超过8 000元，那么该商店至多购进A种纪念品几件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个容量为50的样本中，数据的最大值是123，最小值是45，若取每组终点值与起点值的差为10，则该样本可以分（　　）
    A.5组或6组
    B.6组或7组
    C.7组或8组
    D.8组或9组

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC的两个内角∠A=30°，∠B=70°，则△ABC是( )

    A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形

    查看答案和解析>>

    同步练习册答案