
【题目】如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=6,BC=8,tanD=2,点E是射线CD上一动点(不与点C重合),将△BCE沿着BE进行翻折,点C的对应点记为点F.
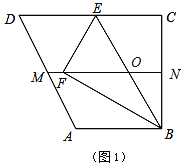
(1)如图1,当点F落在梯形ABCD的中位线MN上时,求CE的长.
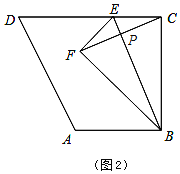
(2)如图2,当点E在线段CD上时,设CE=x,![]() ,求y与x之间的函数关系式,并写出定义域.
,求y与x之间的函数关系式,并写出定义域.
(3)如图3,联结AC,线段BF与射线CA交于点G,当△CBG是等腰三角形时,求CE的长.

【答案】(1)![]() ;(2)
;(2)![]() (0<x≤10);(3)CE的长为
(0<x≤10);(3)CE的长为![]() 或
或 ![]() 或
或![]() .
.
【解析】
(1)把BE与MN的交点记为点O,根据折叠的性质以及梯形中位线定理,可判定△EFO是等边三角形,即可得出∠FEB=60°,即∠CEB=60°,进一步在Rt△ECB中,利用60°角的三角函数即可求出EC的长;
(2)把BE与CF的交点记为点P,根据BE是CF的垂直平分线,可得![]() ,易证△ECP∽△CBP,然后利用相似三角形的性质即可得出y与x之间的函数关系式;
,易证△ECP∽△CBP,然后利用相似三角形的性质即可得出y与x之间的函数关系式;
(3)当△CBG是等腰三角形时,分三种情况进行讨论:①GB=GC;②CB=CG;③BC=BG,分别根据折叠的性质以及直角三角形的边角关系,求得CE的长.
解:(1)把BE与MN的交点记为点O,如图1,
∵梯形ABCD中,AB∥CD,∠ABC=90°,∴∠C=90°,
由翻折得∠CEB=∠FEB,∠EFB=∠C=90°,
∵MN是梯形ABCD的中位线,∴MN∥AB∥CD,
∴∠CEB=∠FOE,![]() ,
,
∴∠FEB=∠FOE,∴FE=FO,
∵∠EFB=90°,EO=BO,∴FO=EO,
∴FE=FO=EO,∴△EFO是等边三角形,
∴∠FEB=60°,∴∠CEB=60°,
∴在Rt△ECB中,![]() ;
;
(2)把BE与CF的交点记为点P,如图2,
由翻折得,BE是CF的垂直平分线,
即∠EPC=∠BPC=90°,![]() ,
,
∴S△EFC=2S△EPC,S△BFC=2S△BPC,
∴![]() ,
,
∵∠ECP+∠BCP=90°,∠CBP+∠BCP=90°,∴∠ECP=∠CBP,
又∵∠EPC=∠BPC=90°,∴△ECP∽△CBP,
∴![]()
∴![]() (0<x≤10);
(0<x≤10);
(3)当△CBG是等腰三角形时,存在三种情况:
①当GB=GC时,延长BF交CD于点H,如图3,
∵AB=6,BC=8,∠ABC=90°,∴AC=10,
∵GB=GC,∴∠GBC=∠GCB,
∵∠HCB=90°,∴∠CHB+∠GBC=90°,
∵∠ABC=90°,∴∠CAB+∠GCB=90°,
∴∠CHB=∠CAB,∴![]() ,
,
∵∠ABC=90°,∴∠ACB+∠CAB=90°,∠ABG+∠GBC=90°,
∴∠CAB=∠GBA,∴GA=GB,∴GA=GC,
∵AB∥CD,∴![]() ,∴CH=AB=6,
,∴CH=AB=6,
∵CE=x,∴EF=x,HE=6﹣x,
∵∠HFE=90°,∴![]() ,
,
解得![]() ,即
,即![]() ;
;
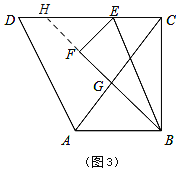
②当CB=CG=8时,AG=10﹣8=2,
∵AB∥CD,∴![]() ,∴CH=4AB=24,
,∴CH=4AB=24,
∵CE=x,∴EF=x,HE=24﹣x,
∵∠HFE=∠HCB=90°,∴![]() ,
,
解得![]() ,即
,即![]() ;
;
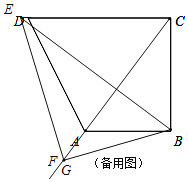
③当BC=BG时,F点与G点重合,如备用图,
由翻折可得,BE垂直平分线段GC,
∵∠CBE+∠BCA=90°=∠CAB+∠BCA,∴∠CBE=∠CAB,
∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,
综上所述,CE的长为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知:二次函数y=x2+bx的图象交x轴正半轴于点A,顶点为P,一次函数y=![]() x﹣3的图象交x轴于点B,交y轴于点C,∠OCA的正切值为
x﹣3的图象交x轴于点B,交y轴于点C,∠OCA的正切值为![]() .
.
(1)求二次函数的解析式与顶点P坐标;
(2)将二次函数图象向下平移m个单位,设平移后抛物线顶点为P′,若S△ABP=S△BCP,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,连接AD交线段PQ于点E,且![]() ,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.
,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.
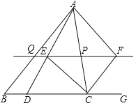
(1)求证:PC=PE;
(2)当P是边AC的中点时,求证:四边形AECF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,点E在边BC上,AE=BE,点M是AE的中点,联结CM,点G在线段CM上,作∠GDN=∠AEB交边BC于N.

(1)如图2,当点G和点M重合时,求证:四边形DMEN是菱形;
(2)如图1,当点G和点M、C不重合时,求证:DG=DN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,BC=3,AC=4,BD平分∠ABC,将△ABC绕着点A旋转后,点B、C的对应点分别记为B1、C1,如果点B1落在射线BD上,那么CC1的长度为_____.
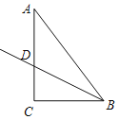
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
(1)求点A,点B的坐标;
(2)P为第二象限抛物线上的一个动点,求△ACP面积的最大值.
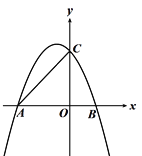
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,
,![]() ,点P为AB边上的一个动点,点E、F分别是CA,CB边的中点,过点P作
,点P为AB边上的一个动点,点E、F分别是CA,CB边的中点,过点P作![]() 于D,设
于D,设![]() ,图中某条线段的长为y,如果表示y与x的函数关系的大致图象如图2所示,那么这条线段可能是
,图中某条线段的长为y,如果表示y与x的函数关系的大致图象如图2所示,那么这条线段可能是![]()
![]()
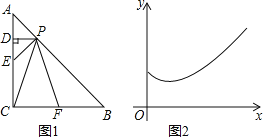
A. PDB. PEC. PCD. PF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的函数,如表是
的函数,如表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小明根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行了探究.
之间的变化规律,对该函数的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:

(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①![]() 对应的函数值
对应的函数值![]() 约为 ;
约为 ;
②该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定抛物线![]() 与
与![]() 轴有两个不同的交点
轴有两个不同的交点![]() ,
,![]() 时,线段
时,线段![]() 称为该抛物线的“横截弦”,其长度记为
称为该抛物线的“横截弦”,其长度记为![]() .
.
(1)已知抛物线![]() ,则
,则![]() ;
;
(2)已知抛物线![]() 经过点
经过点![]() ,当
,当![]() 时,求该抛物线所对应的函数解析式;
时,求该抛物线所对应的函数解析式;
(3)已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
①抛物线恒存在“横截弦”,求![]() 的取值范围;
的取值范围;
②求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
③连接![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .当
.当![]() 时,请直接写出
时,请直接写出![]() 取值范围.
取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com