
【题目】我们规定抛物线![]() 与
与![]() 轴有两个不同的交点
轴有两个不同的交点![]() ,
,![]() 时,线段
时,线段![]() 称为该抛物线的“横截弦”,其长度记为
称为该抛物线的“横截弦”,其长度记为![]() .
.
(1)已知抛物线![]() ,则
,则![]() ;
;
(2)已知抛物线![]() 经过点
经过点![]() ,当
,当![]() 时,求该抛物线所对应的函数解析式;
时,求该抛物线所对应的函数解析式;
(3)已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
①抛物线恒存在“横截弦”,求![]() 的取值范围;
的取值范围;
②求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
③连接![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .当
.当![]() 时,请直接写出
时,请直接写出![]() 取值范围.
取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或y=
或y=![]() ;(3)①
;(3)①![]() ;②当
;②当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;③
;③![]() 或
或![]() ;
;
【解析】
(1)令y=0,得2x2-x-3=0,解得,x1=-1,![]() ,得d=|x1-x2|=
,得d=|x1-x2|=![]() ;
;
(2)经过点A(1,0),d=2,则抛物线与x轴另一个交点是(-1,0)或(3,0),分别代入解析式即可求y=-2x2+2或y=![]() ;
;
(3)将A(1,0)代入y=-x2+bx+c得b+c=1;①抛物线恒存在“横截弦”,△=(1-c)2+4c=c2+2c+1>0;②![]() ,当c>-1时,d=c+1,当c<-1时,d=-c-1;③
,当c>-1时,d=c+1,当c<-1时,d=-c-1;③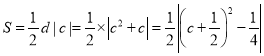 ,1≤S≤10,-5≤c≤-2或1≤c≤4;
,1≤S≤10,-5≤c≤-2或1≤c≤4;
解:(1)令![]() ,得
,得![]() ,
,
解得,![]() ,
,![]() ,
,
![]() ,
,
故答案为:![]() ;
;
(2)经过点![]() ,
,![]() ,
,
∴抛物线与![]() 轴另一个交点是
轴另一个交点是![]() 或
或![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
![]() ,
,![]() 或
或![]() ,
,![]() ,
,
![]() 或
或![]() ;
;
(3)将![]() 代入
代入![]() 得
得![]() ;
;
![]() ,
,
令![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
①抛物线恒存在“横截弦”,
![]() ,
,
![]() ;
;
②![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;
;
③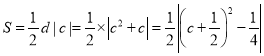 ,
,
![]() ,
,
![]() 或
或![]() ;
;


科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=6,BC=8,tanD=2,点E是射线CD上一动点(不与点C重合),将△BCE沿着BE进行翻折,点C的对应点记为点F.
(1)如图1,当点F落在梯形ABCD的中位线MN上时,求CE的长.
(2)如图2,当点E在线段CD上时,设CE=x,![]() ,求y与x之间的函数关系式,并写出定义域.
,求y与x之间的函数关系式,并写出定义域.
(3)如图3,联结AC,线段BF与射线CA交于点G,当△CBG是等腰三角形时,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上, 顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为__ _.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了求1+2+22+23+…+22016+22017的值,
可令S=1+2+22+23+…+22016+22017,
则2S=2+22+23+24+…+22017+22018,
因此2S﹣S=22018﹣1,
所以1+22+23+…+22017=22018﹣1.
请你仿照以上方法计算1+5+52+53+…+52017的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程![]() 出现了错误,解答过程如下:
出现了错误,解答过程如下:
方程两边都乘以![]() ,得
,得![]() (第一步)
(第一步)
去括号,得![]() (第二步)
(第二步)
移项,合并同类项,得![]() (第三步)
(第三步)
解得![]() (第四步)
(第四步)
![]() 原方程的解为
原方程的解为![]() (第五步)
(第五步)
(1)小明解答过程是从第_____步开始出错的,这一步正确的解答结果_____,此步的根据是_____.
(2)小明的解答过程缺少_____步骤,此方程的解为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,直线
,直线![]() 与y轴交于点A,与双曲线
与y轴交于点A,与双曲线![]() 交于点
交于点![]() .
.
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若![]() 的面积为6,求直线CD的表达式.
的面积为6,求直线CD的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2-12ax+36a-5的图象在4<x<5这一段位于x轴下方,在8<x<9这一段位于x轴上方,则a的值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线l过点(0,2),且与x轴平行;直线![]() 与y轴交于A点,与直线l交于B点;抛物线
与y轴交于A点,与直线l交于B点;抛物线![]() 的顶点为C.
的顶点为C.
(1)求A,B两点的坐标;
(2)求点C的坐标(用m表示);
(3)若抛物线![]() 与线段AB有公共点,求m的取值范围.
与线段AB有公共点,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com