
分析 (1)当x=110时,求出y,根据收支平衡关系列方程即可求解;
(2)根据毛利润=销售收入-服装成本-员工工资-应支付其它费用列函数关系式;
(3)将函数关系式变形为顶点式,求出最大毛利润,根据题意列不等式求解即可.
解答 解:(1)当x=110时,y=-110+160=50,
设该店员工人数为m人,则
50×100+82m+254=110×50
解得:m=3,
答:该店员工的人数为3人.
(2)W=y(x-100)-82×2-254=(-x+160)(x-100)-418=-x2+260x-16418.
(3)W=-x2+260x-16418=-(x-130)2+482,
所以当x=130时,最大毛利润为:482元,
设至少需t天能还清借款,
则482t≥60000+0.0002×60000t
解得:t≥$\frac{6000}{47}$=127$\frac{31}{47}$≈128.
答:最早需要128天能开始盈利,此时每件服装应定价130元.
点评 本题主要考查了二次函数的应用,在解题时要注意二次函数的知识的综合应用和解题方法是本题的关键,是一道常考题.


科目:初中数学 来源: 题型:解答题
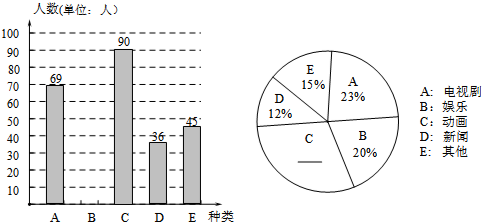
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
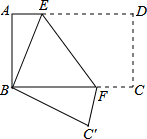 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
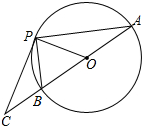 如图,AB为⊙O的直径,直线PC与⊙O相切于点P,交AB的延长线于C,∠PBC=120°,则∠PCB=( )
如图,AB为⊙O的直径,直线PC与⊙O相切于点P,交AB的延长线于C,∠PBC=120°,则∠PCB=( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
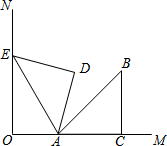 如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.
如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
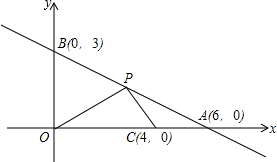 如图,直线AB与x轴、y轴分别交于点A(6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(4,0).
如图,直线AB与x轴、y轴分别交于点A(6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com